LII:Basic Physics of Nuclear Medicine/Computers in Nuclear Medicine
Introduction
[edit | edit source]This is a developing chapter for a Wikibook entitled Basics Physics of Nuclear Medicine.
Computers are widely used in almost all areas of Nuclear Medicine today. The main application for our purposes is imaging acquisition and processing. This chapter outlines the design of a generalised digital image processor and gives a brief introduction to digital imaging.
Before considering these topics, some general comments are required about the form in which information is handled by computers as well as the technology which underpins the development of computers so that a context can be placed on our discussion.
Binary Representation
[edit | edit source]Virtually all computers in use today are based on the manipulation of information which is coded in the form of binary numbers. A binary number can have only one of two values, i.e. 0 or 1, and these numbers are referred to as binary digits – or bits, to use computer jargon. When a piece of information is represented as a sequence of bits, the sequence is referred to as a word; and when the sequence contains eight bits, the word is referred to as a byte – the byte being commonly used today as the basic unit for expressing amounts of binary-coded information. In addition, large volumes of coded information are generally expressed in terms of kilobytes, megabytes etc. It is important to note that the meanings of these prefixes can differ slightly from their conventional meanings because of the binary nature of the information coding. As a result, kilo in computer jargon can represent 1024 units – 1024 (or 210) being the nearest power of 2 to one thousand. Thus, 1 kbyte can refer to 1024 bytes of information and 1 Mbyte can represent 1024 times 1024 bytes. To add a bit of confusion here, some hardware manufacturers refer to a megabyte as 1 million bytes and a gigabyte as a 1,000 million bytes. Its not a simple world, it seems!
Binary coding of image information is needed in order to store images in a computer. Most imaging devices used in medicine however generate information which can assume a continuous range of values between preset limits, i.e. the information is in analogue form. It is therefore necessary to convert this analogue information into the discrete form required for binary coding when images are input to a computer. This is commonly achieved using an electronic device called Analogue-to-Digital Converter (ADC). Furthermore, since many display and photographic devices used in medicine are designed for handling images in analogue format, it is necessary to reconvert the discrete, binary data when outputting images from a computer using a Digital-to-Analogue Converter (DAC).
Development of Modern Computers
[edit | edit source]The development of modern computers has been almost totally dependent on major developments in material science and digital electronics which have occurred over the last thirty years or so. These developments have allowed highly complex electronic circuitry to be compressed into small plastic packages called integrated circuits. These packages contain tiny pieces of silicon (or other semiconductor material) which have been specially manufactured to perform complex electronic processes. The pieces of silicon are generally referred to as silicon chips. Within the circuitry of a chip, a relatively high electronic voltage can be used to represent the digit '1' and a relatively low voltage can be used to represent the binary digit '0'. Thus the circuitry can be used to manipulate information which is coded in the form of binary numbers.
An important feature of these electronic components is the very high speed at which the two voltage levels can be changed in different parts of the circuitry. This results in the ability of the computer to rapidly manipulate the binary information. Furthermore, the tiny size of modern integrated circuits has allowed the manufacture of computers which are very small physically and which do not generate excessive amounts of heat – previous generations of computers having occupied whole rooms, which required cooling because they were built using larger electronic components such as valves and transistors. Thus modern computers are capable of being mounted on a desk in an environment which does not require air-conditioning. In addition, the ability to manufacture integrated circuits using mass production methods has given rise to enormous decreases in costs – which has contributed to the phenomenal explosion of this technology in recent years.
Before beginning, it is worth noting that the information in this chapter is likely to change by the time the chapter is read, given the ongoing, rapid developments in this field. The treatment here is therefore focused on general concepts – and you should note that current technologies and techniques may well differ from those described here. In addition, note that mention of any hardware or software product in this chapter does in no way intend support for such a product and its use in this discussion is purely for illustrative purposes.
Hardware
[edit | edit source]The figure below shows a block diagram of the major hardware components of a general-purpose computer. It shows that a computer consists of a central communication pathway, called a bus, to which dedicated electronic components are connected. Each of these components is briefly described below.

Central Processing Unit (CPU) This component is based, in many modern computers, on an integrated circuit called a microprocessor. Its function is to act as the brains of the computer where instructions are interpreted and executed, and where data is manipulated. The CPU typically contains two sub-components – the Control Unit (CU) and the Arithmetic/Logic Unit (ALU).
The Control Unit is used for the interpretation of instructions which are contained in computer programs as well as the execution of such instructions. These instructions might be used, for example, to send information to other components of the computer and to control the operation of these other components. The ALU is primarily used for data manipulation using mathematical techniques – for example, the addition or multiplication of two numbers.
Important features of individual microprocessors include word length, architecture, programming flexibility and speed. An indicator of speed is the clock rate and values for common microprocessors are given in the following table. Note that the clock rate on its own does not provide a complete indication of computer performance since the specifications of other components must also be considered.
| Microprocessor | Manufacturer | Clock Rate (MHz) | Example Microcomputer |
|---|---|---|---|
| Pentium | Intel | 60-200 | IBM-PC Compatible |
| PowerPC 604e | Motorola | 160-350 | Power Macintosh |
| Turbo SPARC | Sun | 170 | SPARC Station 5 |
| STP1031LGA | Sun | 250 | Ultra SPARC II |
| Pentium II | Intel | 233-450 | IBM-PC Compatible |
| PowerPC 750 | Motorola | 233-500 | Power Macintosh |
| Alpha 21164 | DEC | 300-625 | DEC Alpha |
| Pentium 4 | Intel | 1,300-1,700 | IBM-PC Compatible |
Main Memory
This component typically consists of a large number of integrated circuits which are used for the storage of information which is currently required by the computer user. The circuitry is generally of two types – Random Access Memory (RAM) and Read Only Memory (ROM). RAM is used for the short-term storage of information. It is a volatile form of memory since its information contents are lost when the electric power to the computer is switched off. Its contents can also be rapidly erased – and rapidly filled again with new information. ROM, on the other hand, is non-volatile and is used for the permanent storage of information which is required for basic aspects of the computer's operation.
Secondary Memory
This component is used for the storage of information in permanent or erasable form for longer-term purposes, i.e. for information which is not currently required by the user but which may be of use at some later stage. There are various types of devices used for secondary memory and some of their features are summarised in the following table. RAM is also included in the table for comparison.
The type of technology used is generally based on magnetic materials – similar to those used for sound recording in hi-fi systems. Here, the information is stored by controlling the local magnetism at different points of the storage material and is retrieved by detecting this magnetism. The local magnetism, as might be expected, can assume one of two magnetic states because of the binary nature of the coded information. Materials such as plastic tapes and disks, which have been coated with a layer of magnetic material, are used. Magnetic tapes generally consist of open reels or enclosed cassettes, while magnetic disks generally consist of flexible (or floppy) disks or disks made from a harder plastic. Floppy disks, like magnetic tapes, can be removed from the computer system and are used for external storage of information. Memory sticks can also be used for this purpose. They also allow the capability of transporting information between computers. Hard disks, on the other hand, are usually fixed inside the computer and thus cannot be easily removed – although removable versions are also in use, e.g. the iPod and similar devices.
| Device | Capacity (Mbyte) | Access Time | Erasable? |
|---|---|---|---|
| Magnetic Tape | 500-16,000 | minutes | Yes |
| Floppy Disk | 0.3-1.5 | 200-500 ms | Yes |
| Hard Disk | 1,000-300,000 | 20-80 ms | Yes |
| Removable Hard Disk | 100-100,000 | 100-200 ms | Yes |
| Optical Disk | 250-4,700 | 100-500 ms | Yes/No |
| RAM | 256-4,000 | 10-100 ns | Yes |
Recent developments in our understanding of magnetic and optical characteristics of materials has led to the production of the so-called optical disk – which is similar to the compact disk (CD) used in hi-fi systems. Three general types of optical disk are available: those containing programs supplied by software companies (as in the CD-ROM disk), those which can be written to once by the user (as in the CD-R disk) and those which are erasable (as in the CD-RW disk and the magneto-optical disk). The Digital Versatile Disk (DVD) is a likely successor to the CD-ROM – the first generation having a storage capacity of 4,700 Mbyte (4.7 Gbyte) and the second generation an expected 17,000 Mbyte (17 Gbyte).
A general difference between tape and disk as a secondary storage medium results from the sequential nature of the access to information stored on tape, in contrast to the random nature of the access provided by disks. As a result, disk-based media are typically faster for information storage/retrieval than those based on tape. A number of modern designs of secondary memory are therefore based on hard magnetic disks for routine information storage, with floppy disks used for back-up storage of small volumes of information and optical disks for back-up storage of larger volumes of information.
Input/Output Devices
These components are used for user-control of the computer and generally consist of a keyboard, display device and printer. A wide range of technologies are used here – the details however are beyond the scope of this chapter. These components also include devices such as the mouse, joystick and trackpad, which are used to enhance user-interaction with the computer.
Computer Bus
This consists of a communication pathway for the components of the computer – its function being somewhat analogous to that of the central nervous system. The types of information communicated along the bus include that which specifies data and control instructions as well as the memory addresses where information is to be stored/retrieved. As might be anticipated, the speed at which a computer operates is dependent on the speed at which this communication link works. This speed must be compatible with that of other components, such as the CPU and main memory.
Software
[edit | edit source]There is more to computer technology than just the electronic hardware. In order for the assembly of electronic components to operate, information in the form of data and computer instructions is required. This information is generally referred to as software. Computer instructions are generally contained within computer programs.
Categories of computer program include:
- Operating systems – which are used for operating the computer and for managing various resources of the computer. Examples of operating systems are Windows, MacOS X, Linux and UNIX;
- Application packages – which are for the use of routine users of the computer. These packages include programs which are used for word-processing (e.g. MS Word), spreadsheets (e.g. MS Excel), databases (e.g. FileMaker Pro), graphics (e.g. Adobe Illustrator) and digital image processing (including software used for operating specific medical imaging scanners);
- Programming packages – which are used for writing programs. Examples of common computer languages which are used for writing programs are C (and its many variants) and Java. A number of additional pieces of software are required in order for such programs to be written. These include:
- An Editor for writing the text of the program into the computer (which is similar to programs used for word-processing);
- A Library of subroutines – which are small programs for operating specific, common functions;
- A Linker which is used to link the user-written program to the subroutine library;
- A Compiler or Interpreter for translating user-written programs into a form which can be directly understood by the computer, i.e. it is used to code the instructions in digital format.
- These programming functions and more are combined in packages which generate an Integrated Development Environment (IDE), a good example being Xcode.
Digital Image Processor
[edit | edit source]Computers used for digital image processing generally consist of a number of specialised components in addition to those used in a general-purpose computer. These specialised components are required because of the very large amount of information contained in images and the consequent need for high capacity storage media as well as very high speed communication and data manipulation capabilities. Digital image processing involves both the manipulation of image data and the analysis of such information. An example of image manipulation is the computer enhancement of images so that subtle features are displayed with greater clarity. An example of image analysis is the extraction of indices which express some functional aspect of an anatomical region under investigation. Most medical imaging systems provide extensive image manipulation capabilities with a limited range of image analysis features. Systems for processing nuclear medicine images (including SPECT and PET) also provide extensive data analysis capabilities. This situation arises because of the functional, in contrast to an anatomical, emphasis in nuclear medicine.
A generalised digital image processor is shown in the following figure. The shaded components at the bottom of the diagram are those of a general-purpose computer which have been described above. The digital image processing components are those which are connected to the image data bus. Each of these additional components is briefly described below. The shaded components at the top of the diagram are external devices which are widely used in medical imaging systems.

Imaging System This is the device which produces the primary image information. Examples of these devices include CT scanners, ultrasound machines, x-ray fluorography systems, MRI systems, gamma cameras, PET scanners and computed radiography systems. The device is often physically separate from the other components as in the CT scanner, but may also be mounted in the same cabinet as the other components – as is the case for ultrasound machines. Image information produced by the imaging system is fed to the image acquisition circuitry of the digital image processor.
Connections from the digital image processor to the imaging system are generally also present, for controlling specific aspects of the operation of the imaging system, e.g. gantry movement of a SPECT camera. These additional connections are not shown in the figure for reasons of clarity.
Image Acquisition
This component is used to convert the analogue information produced by the imaging system so that it is coded in the form of binary numbers. The type of device used for this purpose is called an Analogue-to-Digital Converter (ADC). The image acquisition component may also include circuitry for manipulating the digitised data so as to correct for any imaging aberrations. The type of device which can be used for this purpose is called an Input Look-Up Table. Examples of this type of data manipulation include pre-processing functions on ultrasound machines and logarithmic image transformation in digital fluorography systems.
Image Display
This component is sometimes referred to as a display controller and its main use is to convert digital images into a form which is suitable for a visual display device. It includes a Digital-to-Analogue Converter (DAC) when a CRT monitor is used, for instance, and a digital visual interface (DVI) when a digital display such as an LCD monitor is used. The image display component can also include circuitry for manipulating the displayed images so as to enhance their appearance. The type of device which can be used for this purpose is called an Output Look-Up Table. Examples of this type of data manipulation include post-processing functions on ultrasound machines and windowing functions on Nuclear Medicine systems. Other forms of image processing provided by the image display component can include image magnification, image rotation/mirroring and the capability of displaying a number of images on one screen. This component can also allow for the annotation of displayed images with the patient name and details relevant to the patient's examination.
Image Memory
This component typically consists of a volume of RAM which is sufficient for the storage of a number of images which are of current interest to the user.
Image Storage
This component generally consists of magnetic disks of sufficient capacity to store large numbers of images which are not of current interest to the user and which may be transferred to image memory when required.
Image ALU
This component consists of an ALU designed specifically for handling image data. It is generally used for relatively straight-forward calculations, such as image subtraction in DSA and the reduction of noise through averaging a sequence of images.
Array Processor
This component consists of circuitry designed for more complex manipulation of image data and at higher speeds than the Image ALU. It typically consists of an additional CPU as well as specialised high speed data communication and storage circuitry. It may be viewed as a separate special-purpose computer whose design has traded a loss of operational flexibility for enhanced computational speed. This enhanced speed is provided by the capability of manipulating data in a parallel fashion as opposed to a sequential fashion (which is an approach widely used in general-purpose computing). This array processor is used, for example, for calculating Fast Fourier Transforms and for image reconstruction calculations in cross-sectional imaging modalities, such as CT, SPECT and MRI.
Image Data Bus
This component consists of a very high speed communication link designed specifically for image data.
Digital Imaging
[edit | edit source]The digitisation of images generally consists of two concurrent processes – sampling and quantisation. These two processes are described briefly below and a consideration of the storage requirements for digital images follows.
Image Sampling
This process is used to digitise the spatial information in an image. It is typically achieved by dividing an image into a square or rectangular array of sampling points. Each of the sampling points is referred to as a picture element – or pixel to use computer jargon.

The process may be summarised as the digitisation of an analogue image into an N x N array of pixel data. Examples of values for N are 128 for a nuclear medicine scan, 512 for CT and MRI scans, 1024 for a DSA image, and 2048 for a computed radiograph image and digital radiograph. Note that N has values which are integer powers of 2, because of the binary nature of modern computing techniques.
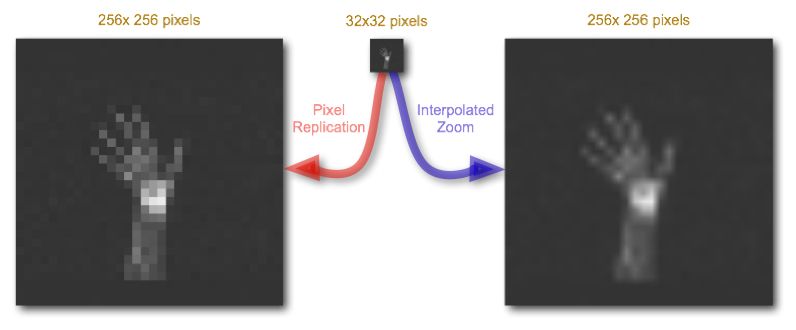
Naturally, the larger the number of pixels, the closer the spatial resolution of the digitised image approximates that of the original analogue image – see the images below.
Image Quantisation
This process refers to the digitisation of the brightness information in an image. It is typically achieved by representing the brightness of a pixel by an integer whose value is proportional to the brightness. This integer is referred to as a 'pixel value' and the range of possible pixel values which a system can handle is referred to as the gray scale. Naturally, the greater the gray scale, the closer the brightness information in the digitised image approximates that of the original, analogue image – see the images below.
The process may be considered as the digitisation of image brightness into G shades of gray. The value of G is dependent on the binary nature of the information coding. Thus G is generally an integer power of 2, i.e. G=2 m, where m is an integer which specifies the number of bits required for storage. Examples of values of G are 256 (m=8) in ultrasonography, 1024 (m=10) in DSA and 4096 (m=12) in nuclear medicine.

Digital Image Resolution
The number of bits, b, required to represent an image in digital format is given by
The following table shows the number of bits required to represent images which are digitised at different spatial resolutions for a range of gray scales. It is seen that very large values are required to achieve the resolution used in medical imaging (you might confirm as an exercise that the asterisked value in the Table represents 0.25 Mbytes). The resulting amounts of computer memory needed to store such images are therefore quite large and processing times can be relatively long when manipulating such large volumes of data. This feature of digital images gives rise to the need for dedicated hardware for image data which is separate from the components of a general-purpose computer as we have described above – although this distinction is vanishing with ongoing technological developments.
| N x N | m = 8 | m = 10 | m = 12 |
|---|---|---|---|
| 128 x 128 | 131,072 | 163,840 | 196,608 |
| 256 x 256 | 524,288 | 655,360 | 786,432 |
| 512 x 512 | 2,097,152* | 2,621,440 | 3,145,728 |
| 1024 x 1024 | 8,388,608 | 10,485,760 | 12,582,912 |
| 2048 x 2048 | 33,554,432 | 41,943,040 | 50,331,648 |
Digital Image Processing
[edit | edit source]Contrast enhancement as an example of a very common form of digital processing of images (also referred to as windowing) is described below. It is just one from the wide range of data manipulation processes which are available on modern systems. Contrast enhancement is a form of gray-level transformation where the real pixel values in an image are replaced by processed pixel values for display purposes.

The process is generally performed using the Output Look-Up Table section of the image display component of the digital image processor. As a result, the original data in image memory is not affected by the process, so that from an operational viewpoint, the original image data can be readily retrieved in cases where an unsatisfactory output image is obtained. In addition, the process can be implemented at very high speed using modern electronic techniques so that, once again from an operational viewpoint, user-interactivity is possible.
An example of a Look-Up Table (LUT) which can be used for contrast enhancement is illustrated in the following figure. This information is usually presented using a graph of the real pixel values stored in image memory versus the pixel values used for display purposes. The process is generally controlled using two controls on the console of the digital image processor – the LEVEL control and the WINDOW control. It should be noted that variations in the names for these controls, and in their exact operation, exist between different systems but the general approach described here is sufficient for our purposes. It is seen the figure that the LEVEL controls the threshold value below which all pixels are displayed as black and the WINDOW controls a similar threshold value for a white output. The simultaneous use of the two controls allows the application of a gray-level window, of variable width, which can be placed anywhere along the gray scale. Subtle gray-level changes within images can therefore be enhanced so that they are displayed with greater clarity. A common application of this form of digital image processing in nuclear medicine is the removal of background counts from images.
Other forms of contrast enhancement used in Nuclear Medicine include using LUTs with logarithmic, exponential or other nonlinear input/output relationship – the logarithmic LUT being used for instance to accommodate a broad range of counts on one grey scale. Colour LUTs are also popular, where the digital contrast resolution of an image is represented by a range of different colours – a rainbow scheme for example as shown in the following figure – or by hues of one or a small number of colours.

|

|

|
The red, green and blue channels are represented by the plots with the respective colours.
Click HERE to view a QuickTime movie (~9 Mbyte) demonstrating the effects of various CLUTs on a fused SPECT/CT study.
Other examples of digital image processing are illustrated in figure below:

A detailed treatment of the image processing capabilities of a modern personal computer is provided at this external link.
Other common forms of digital image processing include applying geometric transformations to images so as to magnify or zoom in on specific details or to correct for geometric distortions introduced by the imaging system. Image zoom can be readily achieved in the display controller using a pixel replication process, where each pixel is displayed N2 times, where N is the zoom factor, as illustrated below:

A disadvantage of this approach however is that zoomed images can have a blocky appearance reflecting the larger size of each effective pixel. Although the application of a smoothing filter can reduce this pixelation effect, a more visually pleasing result can be generated using spatial interpolation techniques. Here, the pixel values of unknown pixels are estimated using the pixel values of known neighbouring pixels. Suppose the image above is zoomed again and suppose that this time the known pixels are distributed to the corners of the zoomed image, as shown in the following figure:

The task of the interpolation process is to calculate the pixel values of the unknown pixels based on the known pixel values of the corner pixels. The simplest approach is linear interpolation where a linear relationship between the pixel values of the known pixels is assumed. Let's suppose that we wish to estimate the pixel value of the pixel shaded red in the figure above. In the case of two-dimensional linear interpolation, also called bilinear interpolation, the first step is to calculate the pixel value of the pixel at position (x,0), shaded yellow on the top line of the matrix, as follows:
where x: fractional distance along the horizontal axis.
Similarly, the pixel value of the pixel shaded yellow on the bottom line of the matrix, at position (x,1), is calculated using the following equation:
Finally, the pixel value for the unknown red-shaded pixel in the figure can be obtained by linear interpolation between these two calculated (yellow-shaded) pixel values, as follows:
where y: fractional distance along the vertical axis.
This process is applied to all unknown pixels in an image. Example images are shown below:
Functions other than linear can also be applied, e.g. two-dimensional polynomial and cubic spline interpolation, to effect a more visually pleasing result. Remember however that the interpolated data is not real and the approach simply generates estimates of pixel values in an effort to improve the blocky nature of the simple zoom technique considered earlier. We'll be considering further applications of image interpolation in our chapter on X-ray CT.
The Fourier Transform – A Pictorial Essay
[edit | edit source]The treatment of the Fourier Transform (FT) in many textbooks uses a level of mathematics which is quite alien to many students of the medical sciences. The treatment here will adopt a different approach, based on a pictorial essay, in an attempt to convey more effectively the concept on which the transform is based. It does in no way substitute for a rigorous mathematical treatment, and is solely aimed at supporting your understanding of image filtering.

This presentation will demonstrate that images can be thought about from both spatial and spatial frequency perspectives. The spatial perspective is the conventional way of presenting image data and relates to real world parameters such as distance and time. An image may also be considered as consisting of a large number of spatial frequencies interacting with each other. This aspect will be examined using a fairly simple image to begin with, and then by considering a more complicated one, namely a chest radiograph, i.e. an example of medical image which consists of a very broad range of spatial frequencies. The FT transforms the image data from the spatial representation to the spatial frequency representation and the inverse FT performs the reverse operation – see the figure on the right.
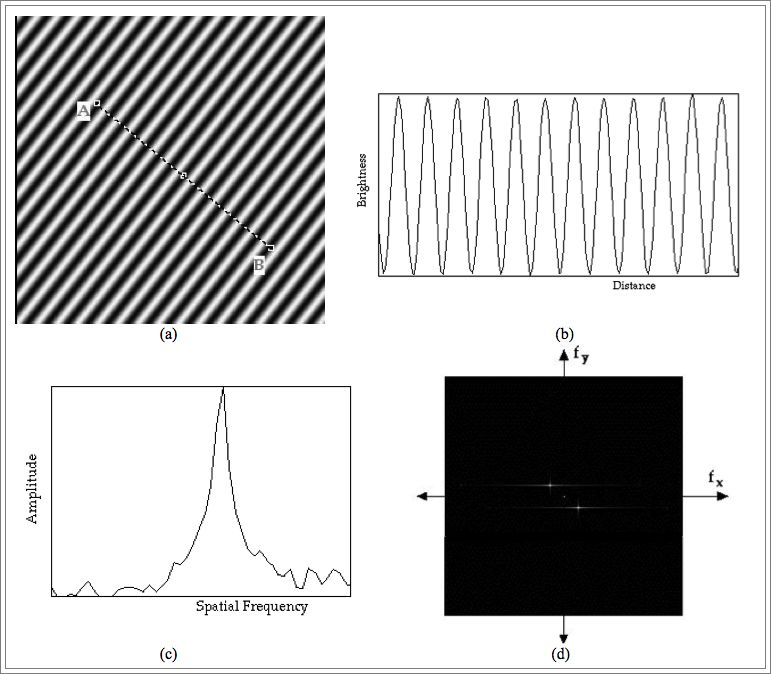
An image of a sinusoidal brightness pattern running at an angle of 45 degrees to the horizontal is shown below in panel (a). A plot of pixel values along the line AB demonstrates this sinusoidal pattern in one dimension as demonstrated in panel (b). It can also be represented in a different fashion by plotting the amplitude of the sine waves present in panel (b) against their spatial frequency. This is shown in panel (c). This latter plot confirms that there is just one spatial frequency dominating the image, as might be expected. This type of plot is called a 1D Fourier spectrum and utilises a one-dimensional FT of the image data. Note that panels (b) and (c) illustrate the frequency information in just one dimension.
When the frequency information is displayed in 2 dimensions, as in panel (d), it is called a 2D Fourier spectrum and this is achieved using a 2D FT of the image data. It demonstrates spatial frequencies for the vertical and horizontal image dimensions along its vertical and horizontal axes, with the origin at the centre (shown by the tiny white dot). Two other dots are seen in panel (d), with slight horizontal streaking beside them – one to the upper left and the other to the bottom right of the origin. These correspond to the frequency of the sine wave in panel (a). Since the FT generates both positive and negative values for the frequency, the resulting two frequencies are displayed on either side of the origin as indicated.
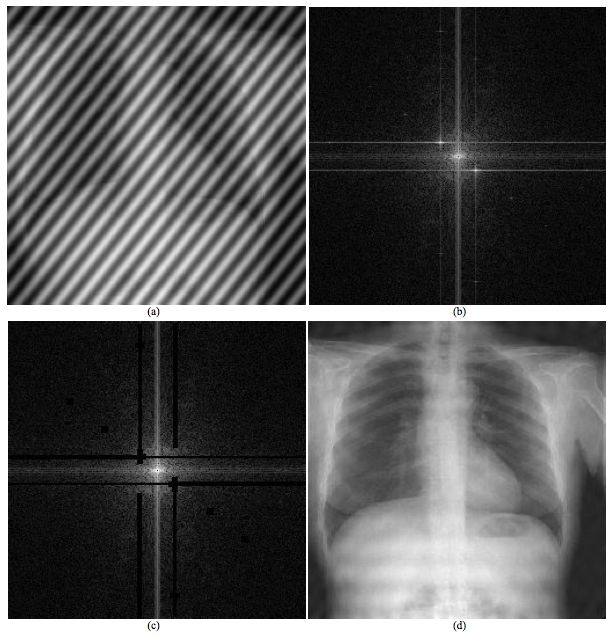
A more complicated 2-D Fourier spectrum is obtained when a chest radiograph is transformed to the spatial frequency domain as illustrated in the next figure. The transformed data show a broad range of spatial frequencies, with significant vertical and horizontal features, as might be expected from the horizontal ribs and vertical vertebral column displayed in the radiograph.

A potential use of the FT and its inverse is the removal of unwanted or corrupt data from a digital image and this process is illustrated in the final figure below. An extreme example of a corrupt image may be generated by adding together the two images just analysed, as in panel (a). The Fourier spectrum in panel (b) portrays the frequency characteristics of the summed image. The undesirable features attributable to the sinusoidal pattern may be removed by editing of the data in the frequency domain as in panel (c), before the inverse FT is performed to recover an image largely free of artifact, as in panel (d).
The key finding to be gleaned from these three examples is that the spatial and spatial frequency representations of the image data are entirely equivalent. The frequency representation has numerous advantages in terms of data manipulation. In general the FT and its inverse provide us with the tools to transform the data from the real world to one of spatial frequency and vice versa.
A more formal treatment of the Fourier transform is presented in our chapter on Fourier Methods.
Notes
This article is a direct transclusion of the Wikibooks article and therefore may not meet the same editing standards as LIMSwiki.