Difference between revisions of "Journal:Data management and modeling in plant biology"
Shawndouglas (talk | contribs) (→Notes: Added cat) |
Shawndouglas (talk | contribs) (→Notes: Cats) |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 19: | Line 19: | ||
|download = [https://www.frontiersin.org/articles/10.3389/fpls.2021.717958/pdf https://www.frontiersin.org/articles/10.3389/fpls.2021.717958/pdf] (PDF) | |download = [https://www.frontiersin.org/articles/10.3389/fpls.2021.717958/pdf https://www.frontiersin.org/articles/10.3389/fpls.2021.717958/pdf] (PDF) | ||
}} | }} | ||
{{ | {{Ombox math}} | ||
}} | |||
==Abstract== | ==Abstract== | ||
The study of plant-environment interactions is a multidisciplinary research field. With the emergence of quantitative large-scale and high-throughput techniques, the amount and dimensionality of experimental data have strongly increased. Appropriate strategies for data storage, [[Information management|management]], and [[Data analysis|evaluation]] are needed to make efficient use of experimental findings. Computational approaches to [[data mining]] are essential for deriving statistical trends and signatures contained in data matrices. Although, current biology is challenged by high data dimensionality in general, this is particularly true for plant biology. As sessile organisms, plants have to cope with environmental fluctuations. This typically results in strong dynamics of metabolite and protein concentrations, which are often challenging to quantify. Summarizing experimental output results in complex data arrays, which need computational statistics and numerical methods for building quantitative models. Experimental findings need to be combined with computational models to gain a mechanistic understanding of plant metabolism. For this, [[bioinformatics]] and mathematics need to be combined with experimental setups in physiology, biochemistry, and molecular biology. This review presents and discusses concepts at the interface of experiment and computation, which are likely to shape current and future plant biology. Finally, this interface is discussed with regard to its capabilities and limitations to develop a quantitative model of plant-environment interactions. | The study of plant-environment interactions is a multidisciplinary research field. With the emergence of quantitative large-scale and high-throughput techniques, the amount and dimensionality of experimental data have strongly increased. Appropriate strategies for data storage, [[Information management|management]], and [[Data analysis|evaluation]] are needed to make efficient use of experimental findings. Computational approaches to [[data mining]] are essential for deriving statistical trends and signatures contained in data matrices. Although, current biology is challenged by high data dimensionality in general, this is particularly true for plant biology. As sessile organisms, plants have to cope with environmental fluctuations. This typically results in strong dynamics of metabolite and protein concentrations, which are often challenging to quantify. Summarizing experimental output results in complex data arrays, which need computational statistics and numerical methods for building quantitative models. Experimental findings need to be combined with computational models to gain a mechanistic understanding of plant metabolism. For this, [[bioinformatics]] and mathematics need to be combined with experimental setups in physiology, biochemistry, and molecular biology. This review presents and discusses concepts at the interface of experiment and computation, which are likely to shape current and future plant biology. Finally, this interface is discussed with regard to its capabilities and limitations to develop a quantitative model of plant-environment interactions. | ||
| Line 109: | Line 105: | ||
===Differential equation models for quantitative analysis of biochemical network dynamics=== | ===Differential equation models for quantitative analysis of biochemical network dynamics=== | ||
Mathematical models of plant metabolism are frequently based on systems of DEs. For example, dynamics of metabolite concentrations are mathematically described in such models by the sum of synthesizing and interconverting/degrading enzyme reactions. Typically, time is considered to be the only independent variable, and, thus, ordinary differential equations (ODEs) are applied for simulating biochemical networks. | Mathematical models of plant metabolism are frequently based on systems of DEs. For example, dynamics of metabolite concentrations are mathematically described in such models by the sum of synthesizing and interconverting/degrading enzyme reactions. Typically, time is considered to be the only independent variable, and, thus, ordinary differential equations (ODEs) are applied for simulating biochemical networks.<ref>{{Cite journal |last=Andrews |first=Steven S. |last2=Arkin |first2=Adam P. |date=2006-07 |title=Simulating cell biology |url=https://linkinghub.elsevier.com/retrieve/pii/S0960982206017751 |journal=Current Biology |language=en |volume=16 |issue=14 |pages=R523–R527 |doi=10.1016/j.cub.2006.06.048}}</ref> If two or more independent variables are considered, e.g., time and space, partial differential equations (PDEs) are applied. | ||
To briefly illustrate the suitability of (ordinary) differential equations for dynamic modeling of metabolism, consider an arbitrary enzyme catalyzed two-substrate reaction: | To briefly illustrate the suitability of (ordinary) differential equations for dynamic modeling of metabolism, consider an arbitrary enzyme catalyzed two-substrate reaction: | ||
| Line 119: | Line 115: | ||
<math>{- \frac{d\left\lbrack A \right\rbrack}{dt} = - \frac{d\left\lbrack B \right\rbrack}{dt} = \frac{d\left\lbrack C \right\rbrack}{dt} = k\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = f\left( {A,B,C} \right)}</math> | <math>{- \frac{d\left\lbrack A \right\rbrack}{dt} = - \frac{d\left\lbrack B \right\rbrack}{dt} = \frac{d\left\lbrack C \right\rbrack}{dt} = k\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = f\left( {A,B,C} \right)}</math> | ||
The right side of the ODEs can be summarized by metabolic functions ''f''(A, B, C) comprising all (kinetic) terms, which contribute to changes in concentration of substrate and product molecules. While in this arbitrary example metabolic functions only comprise one kinetic term, the composition of such functions in metabolic systems are much more complex due to various enzyme reactions, which contribute to synthesis, degradation, or transport of metabolites. Also, while kinetics in this equation are described as constantly proportional to substrate concentrations without regulatory impact, enzyme catalyzed reactions typically follow kinetics with saturation, inhibition, and activation. Systems of DEs mathematically amalgamate different kinetic laws with dynamic substrate, product, and effector concentrations, which enable quantitative simulation of metabolism. Further, DEs enable different types of kinetic modeling focusing on dynamic (time-series) data or steady-state approaches. | The right side of the ODEs can be summarized by metabolic functions ''f''(A, B, C) comprising all (kinetic) terms, which contribute to changes in concentration of substrate and product molecules. While in this arbitrary example metabolic functions only comprise one kinetic term, the composition of such functions in metabolic systems are much more complex due to various enzyme reactions, which contribute to synthesis, degradation, or transport of metabolites. Also, while kinetics in this equation are described as constantly proportional to substrate concentrations without regulatory impact, enzyme catalyzed reactions typically follow kinetics with saturation, inhibition, and activation. Systems of DEs mathematically amalgamate different kinetic laws with dynamic substrate, product, and effector concentrations, which enable quantitative simulation of metabolism. Further, DEs enable different types of kinetic modeling focusing on dynamic (time-series) data or steady-state approaches.<ref>{{Cite journal |last=Rohwer |first=Johann M. |date=2012-03 |title=Kinetic modelling of plant metabolic pathways |url=https://academic.oup.com/jxb/article-lookup/doi/10.1093/jxb/ers080 |journal=Journal of Experimental Botany |language=en |volume=63 |issue=6 |pages=2275–2292 |doi=10.1093/jxb/ers080 |issn=1460-2431}}</ref> However, for simulation of kinetic DE models within physiologically relevant boundaries, sets of kinetic parameters and metabolite concentrations need to be quantified. As a consequence, due to experimental limitations, the applicability of (O)DE-based models is frequently limited to relatively small networks and narrow time frames, in which the model can explain or reliably predict experimental data. Nevertheless, DEs constitute a very important approach for modeling of metabolic networks because of the inbuilt consideration of substrate and product concentrations on metabolic functions, i.e., a changing substrate concentration has a direct effect on its own metabolic function.<ref>{{Cite journal |last=Nägele |first=Thomas |date=2014-11-06 |title=Linking metabolomics data to underlying metabolic regulation |url=http://journal.frontiersin.org/article/10.3389/fmolb.2014.00022/abstract |journal=Frontiers in Molecular Biosciences |volume=1 |doi=10.3389/fmolb.2014.00022 |issn=2296-889X |pmc=PMC4428386 |pmid=25988163}}</ref> | ||
In a metabolic DE model, each differential equation describes dynamics of one metabolite. Thus, modeling a metabolic network results in a system of DEs, which needs to be solved, i.e., numerically integrated, within biochemical and physiological boundaries. Numerical integration of (O)DEs can be performed computationally using platforms like Copasi | In a metabolic DE model, each differential equation describes dynamics of one metabolite. Thus, modeling a metabolic network results in a system of DEs, which needs to be solved, i.e., numerically integrated, within biochemical and physiological boundaries. Numerical integration of (O)DEs can be performed computationally using platforms like Copasi<ref>{{Cite journal |last=Hoops |first=S. |last2=Sahle |first2=S. |last3=Gauges |first3=R. |last4=Lee |first4=C. |last5=Pahle |first5=J. |last6=Simus |first6=N. |last7=Singhal |first7=M. |last8=Xu |first8=L. |last9=Mendes |first9=P. |last10=Kummer |first10=U. |date=2006-12-15 |title=COPASI--a COmplex PAthway SImulator |url=https://academic.oup.com/bioinformatics/article-lookup/doi/10.1093/bioinformatics/btl485 |journal=Bioinformatics |language=en |volume=22 |issue=24 |pages=3067–3074 |doi=10.1093/bioinformatics/btl485 |issn=1367-4803}}</ref><ref>{{Cite journal |last=Kent |first=Edward |last2=Hoops |first2=Stefan |last3=Mendes |first3=Pedro |date=2012-12 |title=Condor-COPASI: high-throughput computing for biochemical networks |url=https://bmcsystbiol.biomedcentral.com/articles/10.1186/1752-0509-6-91 |journal=BMC Systems Biology |language=en |volume=6 |issue=1 |pages=91 |doi=10.1186/1752-0509-6-91 |issn=1752-0509 |pmc=PMC3527284 |pmid=22834945}}</ref>, Python<ref>{{Cite book |last=van Rossum, G.; Drake Jr., F.L. |year=1995 |title=Python Tutorial |publisher=Centrum voor Wiskunde en Informatica |volume=620}}</ref>, or [[R (programming language)|R]].<ref>{{Cite web |last=R Core Team |date=2021 |title=R: A Language and Environment for Statistical Computing |url=https://www.r-project.org/ |publisher=R Foundation for Statistical Computing |accessdate=16 August 2021}}</ref> Boundaries for solving ODEs arise from experiments and typically comprise information about SD/error of kinetic parameters, protein, or metabolite concentration. Within the process of parameter estimation, kinetic parameters are determined to reflect experimental data on metabolite or protein concentrations with a minimized error.<ref>{{Cite journal |last=Moles |first=Carmen G. |last2=Mendes |first2=Pedro |last3=Banga |first3=Julio R. |date=2003-11 |title=Parameter Estimation in Biochemical Pathways: A Comparison of Global Optimization Methods |url=http://genome.cshlp.org/lookup/doi/10.1101/gr.1262503 |journal=Genome Research |language=en |volume=13 |issue=11 |pages=2467–2474 |doi=10.1101/gr.1262503 |issn=1088-9051 |pmc=PMC403766 |pmid=14559783}}</ref> Hence, the more precise experimental quantification of such parameters and concentration is the less ambiguous are solutions of equation systems. Yet, previous findings also indicated that parameter measurements must be highly precise and complete in order to minimize “sloppiness” in parameter sensitivities and to usefully constrain model predictions.<ref>{{Cite journal |last=Gutenkunst |first=Ryan N |last2=Waterfall |first2=Joshua J |last3=Casey |first3=Fergal P |last4=Brown |first4=Kevin S |last5=Myers |first5=Christopher R |last6=Sethna |first6=James P |date=2007-10-05 |editor-last=Arkin |editor-first=Adam P |title=Universally Sloppy Parameter Sensitivities in Systems Biology Models |url=https://dx.plos.org/10.1371/journal.pcbi.0030189 |journal=PLoS Computational Biology |language=en |volume=3 |issue=10 |pages=e189 |doi=10.1371/journal.pcbi.0030189 |issn=1553-7358 |pmc=PMC2000971 |pmid=17922568}}</ref> Based on their findings, the authors suggest to focus rather on validation of model predictions than on model parameters. Although uncertainties about model structure, parameters, or kinetic laws can hardly be excluded from future modeling approaches due to their nested architecture<ref>{{Cite journal |last=Liebermeister |first=W. |last2=Schaber |first2=J. |last3=Klipp |first3=E. |date=2009-01-01 |title=Nested uncertainties in biochemical models |url=https://digital-library.theiet.org/content/journals/10.1049/iet-syb_20070042 |journal=IET Systems Biology |language=en |volume=3 |issue=1 |pages=1–9 |doi=10.1049/iet-syb:20070042 |issn=1751-8849}}</ref>, an iterative workflow consisting of model development, simulation, and validation by quantitative experiments will refine and advance model output and predictive power.<ref>{{Cite journal |last=Babtie |first=Ann C. |last2=Stumpf |first2=Michael P. H. |date=2017-08 |title=How to deal with parameters for whole-cell modelling |url=https://royalsocietypublishing.org/doi/10.1098/rsif.2017.0237 |journal=Journal of The Royal Society Interface |language=en |volume=14 |issue=133 |pages=20170237 |doi=10.1098/rsif.2017.0237 |issn=1742-5689 |pmc=PMC5582120 |pmid=28768879}}</ref> Such modeling approaches have revealed detailed insights into molecular processes comprising, e.g., regulatory motifs of moonlighting proteins<ref>{{Cite journal |last=Krantz |first=Maria |last2=Klipp |first2=Edda |date=2020-01-01 |title=Moonlighting proteins - an approach to systematize the concept |url=https://content.iospress.com/articles/in-silico-biology/isb190473 |journal=In Silico Biology |language=en |volume=13 |issue=3-4 |pages=71–83 |doi=10.3233/ISB-190473 |issn=1386-6338 |pmc=PMC7505007 |pmid=32285845}}</ref>, temperature compensation in reaction networks<ref>{{Cite journal |last=Ruoff |first=Peter |last2=Zakhartsev |first2=Maxim |last3=Westerhoff |first3=Hans V. |date=2007-02 |title=Temperature compensation through systems biology: Temperature compensation of fluxes |url=https://onlinelibrary.wiley.com/doi/10.1111/j.1742-4658.2007.05641.x |journal=The FEBS Journal |language=en |volume=274 |issue=4 |pages=940–950 |doi=10.1111/j.1742-4658.2007.05641.x}}</ref>, or mechanisms regulating diurnal starch dynamics.<ref>{{Cite journal |last=Pokhilko |first=Alexandra |last2=Flis |first2=Anna |last3=Sulpice |first3=Ronan |last4=Stitt |first4=Mark |last5=Ebenhöh |first5=Oliver |date=2014 |title=Adjustment of carbon fluxes to light conditions regulates the daily turnover of starch in plants: a computational model |url=http://xlink.rsc.org/?DOI=C3MB70459A |journal=Mol. BioSyst. |language=en |volume=10 |issue=3 |pages=613–627 |doi=10.1039/C3MB70459A |issn=1742-206X}}</ref> | ||
==Future perspective and conclusion== | |||
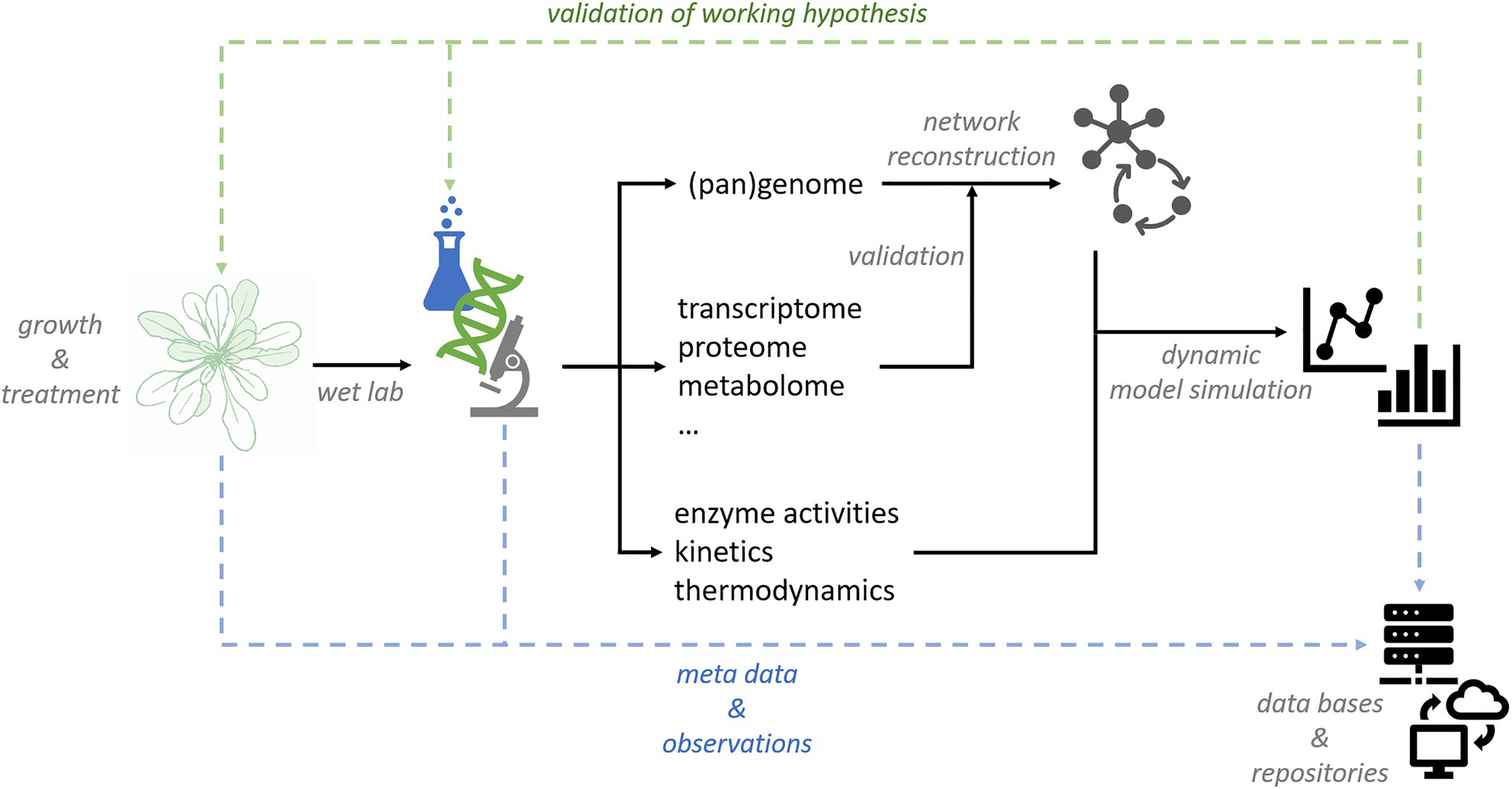
Due to tremendous progress in experimental high-throughput analysis, well conceptualized research data management systems are becoming essential for sustainable data storage and labeling. Simultaneously, quantitative analysis of plant metabolism on large scale will support combination and comparison of complex data originating from different labs or research platforms. Bioinformatics and -mathematics play a central role both in data management and modeling due to their capability to manage, integrate, and analyze multidimensional data sets. In combination with dynamic mathematical models, network structures elucidated by (pan)genome-based network reconstruction will yield mechanistic insight into regulation of plant metabolism (Figure 3). | |||
[[File:Fig3 Krantz FrontPlantSci2021 12.jpg|900px]] | |||
{{clear}} | |||
{| | |||
| style="vertical-align:top;" | | |||
{| border="0" cellpadding="5" cellspacing="0" width="900px" | |||
|- | |||
| style="background-color:white; padding-left:10px; padding-right:10px;" |<blockquote>'''Figure 3.''' Conceptual workflow for data management and modeling in plant sciences.</blockquote> | |||
|- | |||
|} | |||
|} | |||
Finally, beyond its role as a tool for understanding and analyzing experimental data on plant metabolism, mathematical modeling also enables the comparison to structure and regulation of other complex systems in nature and engineering, which will support and accelerate the identification of underlying universal principles of biochemical network organization, regulation, and architecture. | |||
==Acknowledgements== | |||
We thank the members of the SFB/TR175 consortium for many fruitful discussions and DFG for funding. | |||
===Author contributions=== | |||
MK and DZ are first authors and contributed equally to this manuscript. TN conceived and wrote the manuscript. All authors contributed to the article and approved the submitted version. | |||
===Funding=== | |||
This work was funded by Deutsche Forschungsgemeinschaft (DFG), TR175/D02, D03, and INF. | |||
===Conflict of interest=== | |||
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. | |||
==References== | ==References== | ||
| Line 134: | Line 159: | ||
[[Category:LIMSwiki journal articles (with rendered math)]] | [[Category:LIMSwiki journal articles (with rendered math)]] | ||
[[Category:LIMSwiki journal articles on clinical informatics]] | [[Category:LIMSwiki journal articles on clinical informatics]] | ||
[[Category:LIMSwiki journal articles on FAIR data principles]] | |||
[[Category:LIMSwiki journal articles on laboratory management]] | |||
[[Category:LIMSwiki journal articles on pathology informatics]] | [[Category:LIMSwiki journal articles on pathology informatics]] | ||
Latest revision as of 16:37, 29 April 2024
| Full article title | Data management and modeling in plant biology |
|---|---|
| Journal | Frontiers in Plant Science |
| Author(s) | Krantz, Maria; Zimmer, David; Adler, Stephan O.; Kitashova, Anastasia; Klipp, Edda; Mühlhaus, Timo; Nägele, Thomas |
| Author affiliation(s) | Humboldt-Universität zu Berlin, Technische Universität Kaiserslautern, Ludwig-Maximilians-Universität München |
| Primary contact | Email: thomas dot naegele at lmu dot de |
| Editors | Fukushima, Atsushi |
| Year published | 2021 |
| Volume and issue | 12 |
| Article # | 717958 |
| DOI | 10.3389/fpls.2021.717958 |
| ISSN | 1664-462X |
| Distribution license | Creative Commons Attribution 4.0 International |
| Website | https://www.frontiersin.org/articles/10.3389/fpls.2021.717958/full |
| Download | https://www.frontiersin.org/articles/10.3389/fpls.2021.717958/pdf (PDF) |
|
|
This article contains rendered mathematical formulae. You may require the TeX All the Things plugin for Chrome or the Native MathML add-on and fonts for Firefox if they don't render properly for you. |
Abstract
The study of plant-environment interactions is a multidisciplinary research field. With the emergence of quantitative large-scale and high-throughput techniques, the amount and dimensionality of experimental data have strongly increased. Appropriate strategies for data storage, management, and evaluation are needed to make efficient use of experimental findings. Computational approaches to data mining are essential for deriving statistical trends and signatures contained in data matrices. Although, current biology is challenged by high data dimensionality in general, this is particularly true for plant biology. As sessile organisms, plants have to cope with environmental fluctuations. This typically results in strong dynamics of metabolite and protein concentrations, which are often challenging to quantify. Summarizing experimental output results in complex data arrays, which need computational statistics and numerical methods for building quantitative models. Experimental findings need to be combined with computational models to gain a mechanistic understanding of plant metabolism. For this, bioinformatics and mathematics need to be combined with experimental setups in physiology, biochemistry, and molecular biology. This review presents and discusses concepts at the interface of experiment and computation, which are likely to shape current and future plant biology. Finally, this interface is discussed with regard to its capabilities and limitations to develop a quantitative model of plant-environment interactions.
Keywords: genome-scale networks, omics analysis, metabolic regulation, plant-environment interactions, machine learning, mathematical modeling, differential equations
Introduction
Experimental high-throughput analysis of genomes, transcriptomes, proteomes, and metabolomes results in a vast number of simultaneously quantified molecular entities. Current biological research frequently applies a combination of experimental high-throughput techniques to address a wide spectrum of complex research questions. On the genome level, high-throughput sequencing (HTS) technologies have revolutionized genetics and genomics, and sequencing projects have provided comprehensive information about many species’ genomes.[1][2][3][4][5] To date, thousands of genomes have been sequenced and pan-genomics approaches have been initiated, which assemble diverse sets of individual genomes to a collection of all DNA sequences occurring in a species.[6] In plant sciences, the concept of pan-genomics is already discussed to support breeding strategies or evolutionary studies and may significantly contribute to the explanation of gene presence and absence variation.[7]
Based on such comprehensive genome information, genome-scale models of plant metabolism have been developed and applied to predict plant metabolism in a diverse context. Validation and biotechnological application of such large-scale models need appropriate experimental techniques and platforms, unifying sample analysis in multi-omics approaches.[8] Although, omics techniques have become a generic element of numerous research projects to quantify transcripts, proteins, and metabolites, the actual handling, normalization, and integration of multidimensional experimental data output is still a central challenge in biology.[9] The need for integrative analysis of experimental high-throughput data has already been suggested and discussed earlier. For example, almost a decade ago, integrative approaches were suggested for transcriptomics, proteomics, and metabolomics data to promote a systems-level understanding of the genus Arabidopsis.[10] Since then, machine learning, computational statistics, and mathematical modeling have significantly advanced data integration strategies. Due to their capability to improve the understanding of the genotype-phenotype relation on a molecular level, systems biology, and multi-omics integration have become central topics in the discussion about future perspectives of biology and medicine. Yet, in order to make experiments comparable and to increase consistency and reproducibility across different experimental platforms, laboratories, or research communities, quantitative omics data are needed.[11] Furthermore, quantitative experimental data necessitates appropriate processing strategies to make it comparable to other independent studies and statistics. Making data and data processing publicly available via databases and repositories may represent one of the most important steps to establish and expand a cross-disciplinary scientific platform for omics data integration. Together with the need for traceable long-term data storage and versioning, these topics are becoming increasingly important in quantitative biology.
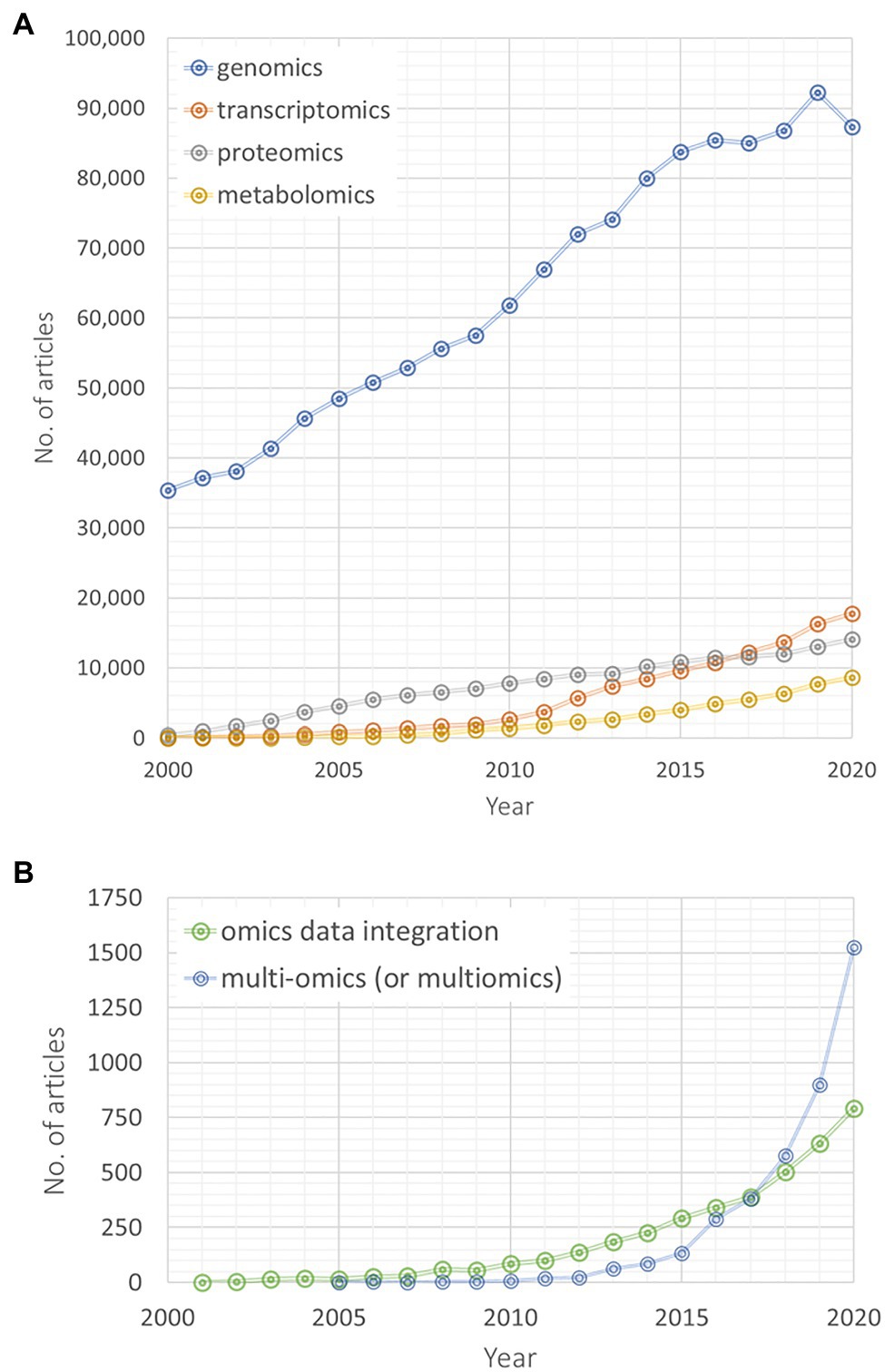
Searching for database entries from the last two decades on omics and integrative omics approaches reveals a rapidly increasing research and publication activity in the integrative multi-omics research field (Figure 1). Genomics-related yearly published articles linearly increased to a very high level during the last 20 years, while particularly transcriptomics and metabolomics articles have been published with an increasing rate during the last decade (Figure 1A). Between 2000 and 2015, more proteomics-related articles have been published than transcriptomics and metabolomics articles, but since 2017 their number lies between both omics disciplines. Interestingly, since 2017, articles searchable by the queries “multi-omics” or “multiomics” are exponentially increasing in their number (Figure 1B). A similar, yet weaker trend is also observable for “omics data integration” articles (Figure 1B). Of course, these numbers are only crude estimates based on our chosen specific vocabulary and searched within one specific database (for example, we have not checked the combination of different omics disciplines, i.e., “genomics” and “transcriptomics” instead of “multi-omics”). Yet, these results still indicate that an increasing number of studies focuses on a multi-omics design and that omics data integration gains more and more attention.
|
This article aims to summarize and discuss current advances and limitations of integrative molecular analysis, computational modeling, and data science. It focuses on both experimental and theoretical methodology to support design and analysis of interdisciplinary research in plant biology. A particular focus is laid on methodologies for capturing system dynamics of plant metabolism induced by a changing environment.
On a large scale: How does genome-scale metabolic network reconstruction support data integration in plant biology?
The availability of comprehensive genome information has enabled the reconstruction of genome-scale metabolic networks, which predict, based on gene annotation, a functional cellular network structure. This crucially supports the interpretation of gene functions and makes pathways accessible to computational biology and mathematics.[12] Further, reconstructed networks significantly facilitate a mechanistic description of genotype-phenotype relationships and enable the application of constraint-based analysis methods.[13][14] Major constraints are thermodynamics, mass and charge conservation, and the substrate/enzyme availability. Constraints dramatically reduce the parameter space, which explains a genotype-phenotype relationship, and, hence, strongly increases the probability to find physiologically relevant solutions for underlying equation systems. Thus, it is not surprising that, in current plant biology, genome-scale reconstruction has become an integral part from single-cell to multi-tissue modeling.[15] For example, model reconstructions have been applied to analyze metabolic regulation in autotrophic and heterotrophic tissues, to study C4 plant metabolism, to evaluate diurnal metabolic interactions in plant leaf tissue and to analyze photorespiration.[16][17][18][19]
The experimental basis for constraining, validating, and optimizing large-scale models are high-throughput experiments, i.e., omics analyses. For example, to investigate effects of nitrogen assimilation on metabolism in maize (Zea mays), a genome-scale metabolic model for maize leaf was created comprising more than 5,800 genes, 8,500 reactions, and 9,000 metabolites.[20] Using a combination of transcriptomic and proteomic data to constrain metabolic flux predictions, the authors were able to reproduce experimentally determined metabolomic data to significantly higher accuracy than without these constraints. Applying a combination of publicly available data on maize metabolism, reaction networks, and results from omics experiments, information about reaction stoichiometry, directionality, and compartmentalization was derived. Algorithmic model curation was combined with manual modification to, for example, resolve gaps in the network model with reactions from similar organisms. Information about transcripts and proteins, which were experimentally observed to significantly differ in mutants and under variable nitrogen supply, were then incorporated into the model by switching on/off corresponding reactions. Flux predictions through the metabolic network were compared to metabolomics measurements. With this integrated setup, model application unraveled genes coding for enzymes, which are involved in regulation of biomass formation under variable nitrogen supply.[20] In another study, publicly available transcriptomics and metabolomics data were used within a constraint-based modeling approach to investigate network structure and flux distribution in root cell types and tissue layers of Arabidopsis thaliana. Based on transcriptomics and metabolomics data, it was possible to extract tissue and cell type specific models from a general genome-scale model of root metabolism. By this, the authors were able to simulate and analyze cell types as autonomous subsystems, which communicate with each other via metabolites or proteins. But it was also shown and discussed that further experimental evidence and constraints are essential to support hypotheses derived from their simulations.[21] This example nicely illustrates how large-scale data integration can (i) unravel novel and detailed mechanistic insights into plant metabolism, and also (ii) indicate design and research focus of follow-up studies to prove model predictions. By placing metabolites, proteins, or transcripts into a pathway and network context, genome-scale models significantly support the biochemical and physiological interpretation of molecular data.
Also, in a biotechnological context, such data integration strategies have become an important and promising tool to advance and improve bioengineering strategies. As an example, a genome-scale metabolic network reconstruction for green microalgal model species Chlamydomonas reinhardtii has been developed which reliably and quantitatively predicts growth depending on the light source.[22] This metabolic network comprises 10 compartments, accounting for more than 1,000 genes associated with more than 2,000 reactions and over 1,000 metabolites. Regulatory effects arising from different light conditions are covered by the model, which enables estimation of growth under different laboratory conditions. The model has been refined using metabolite profiling to include further branches of metabolism, e.g., amino acids and peptides as nitrogen sources.[23] Although, it developed a decade ago, the original model (named iRC1080) still represents a valid and supportive platform for data interpretation, and it still fruitfully initiates further model development and validation.[24] These examples, together with many other studies that have been summarized recently[25], provide strong evidence for the capability of genome-scale metabolic models to couple statistics with metabolic models.
Large-scale models need quantitative large-scale experiments on integrative platforms for validation and iterative parameter optimization
Reconstruction of a genome-scale metabolic network from genome sequence information is an iterative process, which needs several rounds of automatized and manual model adjustment, reconfiguration, and fine-tuning.[26] It strictly depends on genome annotation, and due to the strong increase of genome sequence information, high-throughput annotation algorithms are necessary to cope with this vast amount of data. Particularly in eukaryotic genomes, annotation errors due to assembly errors are still a challenge in the field, and direct RNA sequencing is discussed to improve gene annotation in the future.[27][28] However, as soon as a model has been curated and applied to predict metabolic flux or growth, quantitative experiments are needed to validate the model output, and to iteratively adjust model parameters. In addition to validation variables like growth rates, lipid content, ATP concentration, or total protein amount, experimental omics analyses potentially provide detailed information about pathway regulation, gene regulatory networks, and signaling cascades. Here, mass spectrometry-based proteomics and metabolomics analyses play a crucial role, which are not only able to analyze post-translational modifications or protein localization, but also can quantify turnover rates and metabolic fluxes down to subcellular scale.[29][30]
Quality of experimental data limits optimization of in silico models. If absolute quantitative model predictions about metabolite or protein dynamics cannot be experimentally validated due to missing absolute quantitative experiments, accuracy and reliability of the model frequently remain ambiguous or elusive. Several complex and non-intuitive questions about stability or regulatory patterns might still be addressed with such a model. Yet, the physiological constitution of a plant, or organism in general, which results from a certain growth setup, can hardly be modeled and simulated without quantitative information. For example, plant growth strictly depends on various growth parameters, e.g., light intensity and quality, soil composition, water availability, and humidity. It is well known that a slight modification of only one of those growth parameters might strongly affect the (molecular) phenotype, which makes comparative studies difficult. For example, different light sources might be applied (LEDs, fluorescent tubes, etc.) in different laboratories, which immediately results in different growth behavior and physiological properties.[31] While global harmonization of growth cabinets, greenhouses, or climate chambers remains impractical, augmentation of quantitative omics analysis seems realistic. Recommendations and potential pitfalls of experimental designs are already discussed on a research community level.[11] The authors recommend quality control samples (QCs) and universal standardized operating protocols (SOPs) for quantitative and reproducible experiments. Further, collecting and publishing comprehensive metadata is recommended to guide through and inform about experiments.[32][33][34]
In plant biology, absolute quantification of primary and secondary metabolites might represent a suitable approach to make studies comparable across platforms and growth regimes. Plant metabolism shows a high plasticity across different diurnal light periods. For example, under short day growth conditions with eight hours of light and 16 hours of darkness, dynamics of sugar and amino acid concentrations are significantly stronger than under long day growth conditions, i.e., under 16 hours of light and 8eight hours of darkness.[35] Additionally, the ratio of monosaccharides and disaccharides may vary significantly between growth setups, which is not detectable within a qualitative omics study because it does not allow the absolute comparison of two or more different substances. In mass spectrometry, one reason for this is that different molecules, e.g., sucrose and glucose, produce different ions with different masses, which are detected with different intensity. Hence, to make resulting mass spectra and chromatographic peaks comparable across different substances, they need to be individually scaled by a dilution of standard substances, i.e., within a calibration curve, yielding absolute amount of substance within a sample, which can then be normalized to sample protein amount or sample weight. Depending on the applied growth conditions and treatment, normalization might either be favorable to fresh or dry weight. For example, exposing plants to heat and/or drought stress directly affects leaf water content and, thus, under such conditions normalization to dry weight should be favored if metabolite concentrations are quantified.
While such an approach is appropriate for absolute quantification of central primary metabolites—i.e., sugars, amino acids, or organic acids[36]—it is hardly feasible for each individual substance within a metabolite profile. For many substances, appropriate standard substances are lacking, and even if they are available, they might be expensive due to costly purification and/or synthesis procedures. Further problems might occur when purified substances, like polar and apolar amino acids, need to be diluted and mixed within calibration samples due to their different solubilities in water. The vast number of metabolites, which are estimated to comprise between 200,000 and 1,000,000 across the plant kingdom and up to 5,000 within a single species[37][38], makes quantitative metabolomics challenging. Based on these numbers, it seems unfeasible to resolve the quantity of hundreds or thousands of compounds within a Gas chromatography–mass spectrometry (GC-MS) or Liquid chromatography–mass spectrometry (LC-MS) run. While a combination of different analytical platforms promises to cover a large panel of compounds[39][40], semi-quantitative analysis might represent a suitable approach to increase reproducibility and comparability of high-throughput analysis among quantification platforms. Here, structural elucidation of metabolic compounds based on mass spectrometry data might indicate a compound’s class.[41] This information, together with chromatographic information about retention time or index, might allow classification of an unknown substance by database search and comparison to known substances with similar mass spectra and physical properties like polarity. This would enable the comparison of chromatographic peak areas of an unknown substance to a known and most similar standard substance. For example, an unknown substance which, based on its mass spectrum information, is predicted to be a disaccharide might be semi-quantified applying the calibration of a known disaccharide with similar retention time or index. In this way, semi-quantitative information of an unknown substance might be derived from GC-MS (primary metabolites) or LC-MS (secondary metabolites) runs, which would facilitate comparison and data exchange of independent studies and on different experimental platforms.
Research data management provides the groundwork for successful data integration
Data integration methods, especially machine learning approaches, profit heavily from the increasing availability of data. Aside from high-dimensionality and sparsity of biological data, a fundamental challenge in data integration lies in accessibility and quality of information and knowledge. Modern approaches require not only massive, but particularly well-annotated data sets.[42]
Currently, the default medium of scientific communication in the domain of biology is the publication of research in peer-reviewed scientific journals centered around free text-based communication. While this format has many benefits, such as quality control by curators who are experts on the respective field, it also has the drawback of being gated by pay walls. This issue is already being addressed with the increased founding of open-access journals, but the approach suffers from more intrinsic problems. The format itself was designed as a human-readable medium and is thus prone to design flaws that can be implicitly solved by a human reader but imposes problems to the application of machine learning techniques. Examples being the heterogeneity of supplementals, the embedding of data as schematic descriptions, and most severely, the communication of findings as free text. While these challenges are already identified and currently tackled by manual curation and the application of natural language processing (NLP) and pattern recognition, its frequent occurrence still hinders the direct computational usage of the published knowledge for data integration.[43]
An alternative approach of scientific communication is realized by the creation of knowledge databases. In plant research, there are various information resources and data portals of extremely high quality. UniProt[44] and Ensembl plants[45] are integrative resources presenting genome-scale information for a growing number of sequenced plant species. Additionally, PLAZA[46] provides an integrative resource for functional, evolutionary, and comparative plant genomics. Data portals and specific databases like The Arabidopsis Information Resource (TAIR)[47], Araport[48], Aramemnon[49], or Phytozome[50] provide fine-grained species-specific reference knowledge. Generally, these resources offer a more condensed compilation of knowledge and often preserve the virtue of being manually curated. However, each iteration of a knowledge database only represents a snapshot of the knowledge at the time of creation, which imposes the initiator with the additional burden of maintenance and the user with uncertainty with regards to the currentness of the data source. In comparison to free text, knowledge databases are often easier to access by computational means and provide better interoperability when it comes to the application of machine learning methods; nevertheless, they were and still are designed with a human operator in mind and often lack important metadata information. This does not only affect processes like data retrieval but also the documentation of how data was obtained and integrated when assembling the database.
The communication of findings in scientific publications or their integration in knowledge databases is of course limited by the questions asked at the time of creation. Therefore, best practice suggests publishing raw measurements data in a technology-specific data repository. ProteomeXchange[51], Gene Expression Omnibus (GEO)[52], SRA/ENA[53], and Metabolights[54] are well established data exchange platforms that enforce certain metadata annotation tailored to the individual technology. Generic data repositories like Figshare and Dataverse do not require a technology-specific and laborious annotation process, but in turn do not ensure the necessary metadata annotation. Repositories can improve the process of peer review since the evaluation of data itself can be analyzed with respect to their reproducibility and also make the raw data accessible to the community for reevaluation. This allows the testing of new hypotheses using existing data sets. Nonetheless, the reuse of published data sets is limited by the level of detail in which their creation is described. Therefore, consortia and initiatives coordinate standardization efforts in plant research and developed standards and checklists to formally enable researchers to communicate their findings with required metadata. In the plant field, excellent standardizations for experimental data collections are the Minimal Information on Biological and Biomedical Investigations (MIBBI)[55], Minimal Information About a Microarray Experiment for Plants (MIAME/Plant)[56], and Minimal Information About Plant Phenotyping Experiment (MIAPPE).[57] However, it is exceedingly difficult for researchers to judge the necessity of certain meta information beforehand. Additionally, considerable effort and skills are required to provide adequate metadata annotation to the research data. Researchers also need to allocate the resources and capacity to actually do so in daily research practice. In addition, many researchers view data as sensitive research output that could easily be misused or misinterpreted when taken out of context. Thus, many scientists do not trust global repositories unless they have direct and personal connections to these researchers’ own work or find it too time consuming to validate their trustworthiness.
Nevertheless, it is evident that all ways of research communication (e.g., scientific journals, knowledge databases, and data repositories) heavily benefit from improved metadata description, not only in terms of reproducibility, but also accessibility and thus reusability.[58] It is apparent that research data management requires a constant endeavor of researchers and well accepted standards need to be developed. Here, the FAIR Guiding Principles form a conceptual roof and formulate the necessary goals to achieve. The FAIR Guiding Principles[59] are founded on four core elements: (i) findability, (ii) accessibility, (iii) interoperability, and (iv) re-usability. Findable data is described/annotated with rich metadata and consists of a globally unique identifier, which is indexed in a searchable source, e.g., a database. The metadata must specify what kind of identifier is used. According to accessibility, metadata and data must be retrievable based on their identifier by using a standardized protocol, which is open and universally implementable. Interoperable data use a standard vocabulary based on the FAIR principles and include qualified references to other (meta)data and most importantly are represented using a formal, accessible, shared, and broadly applicable language for knowledge representation. Consequently, re-usable (meta)data have a plurality of accurate and relevant attributes. In addition, they need to be associated with their provenance and meet domain-specific community standards.
Generic implementations to assist researchers abide by the FAIR principles have already been implemented. The usage of Research Object (RO)[60], Research Object Crate (RO-Crate)[61], or ISA data model[62] can lead to a rich description of the experimental metadata (i.e., sample characteristics, technology and measurement types, sample-to-data relationships) that make the resulting data and discoveries reproducible and reusable. Scientific findings accompanied with rich metadata descriptions are representable as knowledge graphs. Such graphs greatly improve their value to the scientific community, since embedding into traversable tree-like structures results in a cross linking of available scientific data, which makes knowledge searchable. In practice, this is achieved using domain specific ontologies, which constrain the used vocabulary and conserve the relationship of single terms.
Reproducibility and provenance play an important role, especially in the computational analysis itself. Recent efforts to make analytic pipelines independent of their runtime environment strongly improved reusability and reproducibility of workflows. Containerization of processing tools and analytic pipelines facilitate the sharing and collaborative development of workflows on specialized platforms like WorkflowHUB. Analogously, computation requires metadata and specifications. In this regard, the BioCompute Object Project[63] aims to ease the exchange of HTS workflows between various organizations by providing a JSON format that, at a minimum, contains all the software versions and parameters necessary to evaluate or verify a computational pipeline.
It becomes evident that a combination of computation, data, and their metadata is essential to achieve the common goal of a well-annotated research object living up to the FAIR principles.[63][64] Therefore, community-driven initiatives like DataPLANT support plant scientists in every research data management concern and provide a tailor-made service environment to contextualize research data according to the FAIR principles with minimal additional effort in modern plant biology.
Recognizing patterns and quantifying dynamics of plant metabolism: Where biology meets mathematics and informatics
Machine learning and its role in quantitative plant biology
The rapid development of experimental high-throughput techniques, together with a significant drop of costs per sample, have made omics analyses become a common element of experimental biology.[8] Resulting data matrices are high-dimensional and, thus, reduction of dimensions to those which explain most of observed variance within a sample set is a routinely applied method. Principal component analysis (PCA) represents a method of unsupervised learning, and, in more detail, it belongs to a branch called distributed representation.[65] Another branch of unsupervised learning frequently applied in biology is clustering. Together with supervised learning and reinforcement learning, unsupervised learning represents a significant sub-discipline of machine learning.[65] Machine learning itself is a subfield of artificial intelligence (AI), which has gained rapidly increasing attention across many biological disciplines during the last decade.[66][67] Supervised and unsupervised learning are two categories of machine learning which differ in the availability, i.e., knowledge, of a response value. In supervised learning, each observation of predictor measurements xi (with observations i=1, …, n), is associated to a response measurement yi. The aim is to fit a model which predicts responses for future observations or which supports the interpretation of predictor-response relationship. In unsupervised learning, predictor measurements xi are available but no response measurements yi. Clustering, as an example for unsupervised learning, aims to figure out whether observations can be separated into distinct groups and, by this, understand the relationship between variables. Reinforcement learning aims to “teach” an agent how to interact with the environment to obtain a “good” score under certain preliminary settings.[68] It plays an important role in many fields of biology, robotics, and health care[69][70] and also gains attention in the field of metabolic engineering. Recently, a reinforcement learning method was applied for bioretrosynthesis, i.e., the synthesis of organic chemicals from low-cost precursors and enzymes.[71]
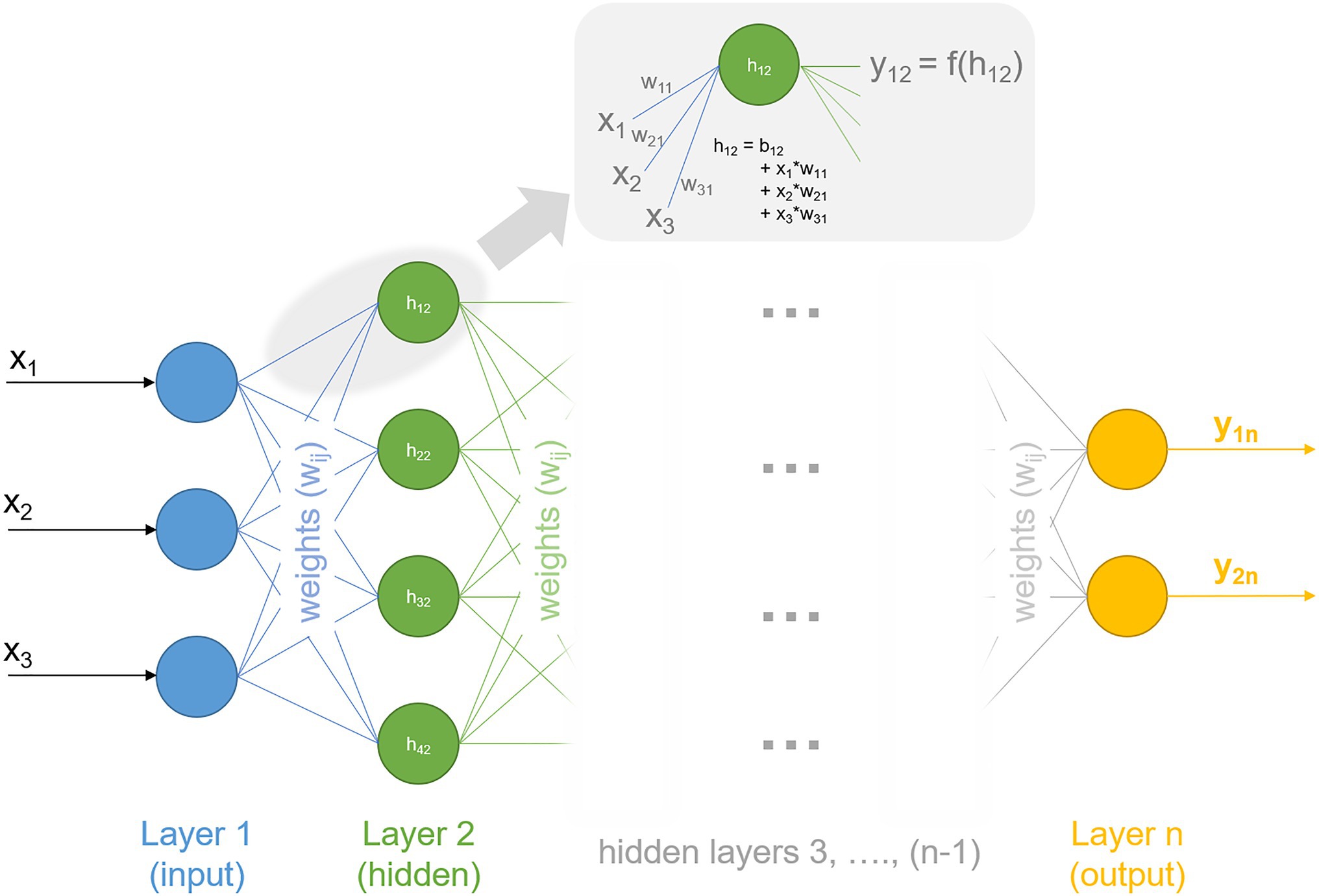
Deep learning is a family of machine learning methods that comprises algorithms of multi-layered artificial neural networks, i.e., in networks of interconnected neurons which are organized within layers. In principle, deep learning approaches also can be subdivided in previously mentioned supervised, unsupervised, and reinforcement learning and extend them to a category in which a model directly learns from a very large data set. Particularly for massive data sets, deep learning performs better than other machine learning approaches.[72] Recently, protein structure prediction has been considerably advanced by the deep learning system AlphaFold, developed by the Google AI offshoot DeepMind.[73] AlphaFold applies deep learning to predict backbone torsion angles and pairwise distances between amino acids within a protein based on sequence information and multiple sequence alignment. In the term "deep learning," "deep" refers to the number of layers of neurons: the more layers, the deeper the network. The flow of information within a neural network starts from neurons within the first layer, the so-called input-layer. Within a fully connected neural network, each neuron of the input-layer is connected to all neurons of the second layer, every second-layer neuron to each third-layer neuron, and so on. Each connection is weighted to determine the quantitative extent to which they are transmitted to the next layer. In addition to weights, each neuron can be modified by a value called bias, which is added to the sum of the previous layer. Hence, applying an (artificial) neural network in data analysis means to search for optimal sets of weights and biases to reduce the error between model output and experimental observation and to maximize probability of true predictions. Typically, nonlinearities (or activation functions) are introduced into the network to describe a transfer function f between layers. For example, nonlinearity converts the input signal of layer 1 into an output signal, which represents the input signal for layer 2 (Figure 2). Weights of the network determine the quantity by which information is passed from layer to layer until the processed information leaves the network by the output layer.
|
This finally represents one central reason why machine learning, and particularly deep learning, are promising and successful strategies for complex, i.e., nonlinear, data analysis: nonlinear functions are employed in different layers to calculate the probability of observing an output due to given input. Examples for such nonlinearities are sigmoid functions and hyperbolic tangent functions.[72] Further, principles like backpropagation are employed for weights learning within an (artificial) neural network, which aim at minimizing error between prediction and observation.[65] Training data sets are applied for the learning process before the network is applied to the test data set, which has not been seen by the model before. This training/test-set validation provides immediate information about the network performance, which is measured by metrics like "R-squared" for regression problems and "the area under the Receiver Operating Characteristic (ROC) curve (auROC)" for classification problems. Also, architecture of neural networks may vary significantly and can, e.g., be discriminated by their number of layers (single or multiple layer width), feedforward (no feedback-loop), or recurrent networks (with at least one feedback-loop within or between layers). The parameter space of neural networks is classified according to their number of layers, the number of neurons within input, hidden and output layers, initial values for weights, initial values for biases, and the occurrence of feedback-loops.
Deep learning has recently gained much attention in the field of plant genomics, proteomics[74], and crop improvement.[25][75] Deep learning models are discussed in context of the new breeding era, Breeding 4.0, which largely depends on genome editing and which would significantly benefit from predictions of allele effects.[75] Predicting how allele effects impact crop yield and general performance under changing environmental conditions would facilitate the identification of molecular traits, which are central for efficient and biomarker-assisted breeding.[75] Although still being very ambitious, with deep learning such predictions become more likely due to the capability of nonlinear data analysis.
In addition to (applied) crop science, machine learning approaches will crucially support basic plant sciences. Particularly, quantitative analysis of nonlinear plant-environment interactions, which essentially shape plant stress response, acclimation, and adaptation, is raised to the next level of complexity.[76] Recent work has indicated how machine learning can be employed to predict plant growth based on reaction rates, which were gained from metabolic models.[77] This shows that machine learning is capable of integrating comprehensive information on different layers of molecular and physiological information. However, it simultaneously emphasizes the need for standardized quantitative high-throughput data for training and testing of machine learning approaches in plant biology.[78] Plant metabolism remains highly complex and machine learning comprises many mathematical functions, which are hardly interpretable with regard to physiology. This might, in some scenarios, even complicate the validation and interpretation of a machine learning-driven prediction because causal inference of molecular processes is prevented by high algorithmic complexity. Furthermore, estimation of performance and accuracy of deep learning models in biology will continuously be limited by experimental data, and plants pose a particular challenge in this context. Their metabolism is highly compartmentalized comprising, compared to animal cells, additional compartments like the vacuole, plastid, and cell wall. Applying combined experimental protocols for subcellular fractionation and omics analysis can provide high-throughput data, which is suitable for quantitative data integration on a large-scale.[79] Finally, plant metabolism is highly dynamic due to diurnal or seasonal changes of the environment, which might be analyzed by differential equation (DE) models, as discussed within the following section.
Differential equation models for quantitative analysis of biochemical network dynamics
Mathematical models of plant metabolism are frequently based on systems of DEs. For example, dynamics of metabolite concentrations are mathematically described in such models by the sum of synthesizing and interconverting/degrading enzyme reactions. Typically, time is considered to be the only independent variable, and, thus, ordinary differential equations (ODEs) are applied for simulating biochemical networks.[80] If two or more independent variables are considered, e.g., time and space, partial differential equations (PDEs) are applied.
To briefly illustrate the suitability of (ordinary) differential equations for dynamic modeling of metabolism, consider an arbitrary enzyme catalyzed two-substrate reaction:
Here, two substrate molecules A and B react to form a product C with the rate constant k. Changes of substrate and product concentrations within a time period Δt (infinitesimally written as dt) are captured by the corresponding ODEs:
The right side of the ODEs can be summarized by metabolic functions f(A, B, C) comprising all (kinetic) terms, which contribute to changes in concentration of substrate and product molecules. While in this arbitrary example metabolic functions only comprise one kinetic term, the composition of such functions in metabolic systems are much more complex due to various enzyme reactions, which contribute to synthesis, degradation, or transport of metabolites. Also, while kinetics in this equation are described as constantly proportional to substrate concentrations without regulatory impact, enzyme catalyzed reactions typically follow kinetics with saturation, inhibition, and activation. Systems of DEs mathematically amalgamate different kinetic laws with dynamic substrate, product, and effector concentrations, which enable quantitative simulation of metabolism. Further, DEs enable different types of kinetic modeling focusing on dynamic (time-series) data or steady-state approaches.[81] However, for simulation of kinetic DE models within physiologically relevant boundaries, sets of kinetic parameters and metabolite concentrations need to be quantified. As a consequence, due to experimental limitations, the applicability of (O)DE-based models is frequently limited to relatively small networks and narrow time frames, in which the model can explain or reliably predict experimental data. Nevertheless, DEs constitute a very important approach for modeling of metabolic networks because of the inbuilt consideration of substrate and product concentrations on metabolic functions, i.e., a changing substrate concentration has a direct effect on its own metabolic function.[82]
In a metabolic DE model, each differential equation describes dynamics of one metabolite. Thus, modeling a metabolic network results in a system of DEs, which needs to be solved, i.e., numerically integrated, within biochemical and physiological boundaries. Numerical integration of (O)DEs can be performed computationally using platforms like Copasi[83][84], Python[85], or R.[86] Boundaries for solving ODEs arise from experiments and typically comprise information about SD/error of kinetic parameters, protein, or metabolite concentration. Within the process of parameter estimation, kinetic parameters are determined to reflect experimental data on metabolite or protein concentrations with a minimized error.[87] Hence, the more precise experimental quantification of such parameters and concentration is the less ambiguous are solutions of equation systems. Yet, previous findings also indicated that parameter measurements must be highly precise and complete in order to minimize “sloppiness” in parameter sensitivities and to usefully constrain model predictions.[88] Based on their findings, the authors suggest to focus rather on validation of model predictions than on model parameters. Although uncertainties about model structure, parameters, or kinetic laws can hardly be excluded from future modeling approaches due to their nested architecture[89], an iterative workflow consisting of model development, simulation, and validation by quantitative experiments will refine and advance model output and predictive power.[90] Such modeling approaches have revealed detailed insights into molecular processes comprising, e.g., regulatory motifs of moonlighting proteins[91], temperature compensation in reaction networks[92], or mechanisms regulating diurnal starch dynamics.[93]
Future perspective and conclusion
Due to tremendous progress in experimental high-throughput analysis, well conceptualized research data management systems are becoming essential for sustainable data storage and labeling. Simultaneously, quantitative analysis of plant metabolism on large scale will support combination and comparison of complex data originating from different labs or research platforms. Bioinformatics and -mathematics play a central role both in data management and modeling due to their capability to manage, integrate, and analyze multidimensional data sets. In combination with dynamic mathematical models, network structures elucidated by (pan)genome-based network reconstruction will yield mechanistic insight into regulation of plant metabolism (Figure 3).
|
Finally, beyond its role as a tool for understanding and analyzing experimental data on plant metabolism, mathematical modeling also enables the comparison to structure and regulation of other complex systems in nature and engineering, which will support and accelerate the identification of underlying universal principles of biochemical network organization, regulation, and architecture.
Acknowledgements
We thank the members of the SFB/TR175 consortium for many fruitful discussions and DFG for funding.
Author contributions
MK and DZ are first authors and contributed equally to this manuscript. TN conceived and wrote the manuscript. All authors contributed to the article and approved the submitted version.
Funding
This work was funded by Deutsche Forschungsgemeinschaft (DFG), TR175/D02, D03, and INF.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- ↑ International Human Genome Sequencing Consortium; Whitehead Institute for Biomedical Research, Center for Genome Research:; Lander, Eric S.; Linton, Lauren M.; Birren, Bruce; Nusbaum, Chad; Zody, Michael C.; Baldwin, Jennifer et al. (15 February 2001). "Initial sequencing and analysis of the human genome" (in en). Nature 409 (6822): 860–921. doi:10.1038/35057062. ISSN 0028-0836. http://www.nature.com/articles/35057062.
- ↑ The 1000 Genomes Project Consortium (1 November 2012). "An integrated map of genetic variation from 1,092 human genomes" (in en). Nature 491 (7422): 56–65. doi:10.1038/nature11632. ISSN 0028-0836. PMC PMC3498066. PMID 23128226. http://www.nature.com/articles/nature11632.
- ↑ Alonso-Blanco, Carlos; Andrade, Jorge; Becker, Claude; Bemm, Felix; Bergelson, Joy; Borgwardt, Karsten M.; Cao, Jun; Chae, Eunyoung et al. (1 July 2016). "1,135 Genomes Reveal the Global Pattern of Polymorphism in Arabidopsis thaliana" (in en). Cell 166 (2): 481–491. doi:10.1016/j.cell.2016.05.063. PMC PMC4949382. PMID 27293186. https://linkinghub.elsevier.com/retrieve/pii/S0092867416306675.
- ↑ Stein, Joshua C.; Yu, Yeisoo; Copetti, Dario; Zwickl, Derrick J.; Zhang, Li; Zhang, Chengjun; Chougule, Kapeel; Gao, Dongying et al. (1 February 2018). "Genomes of 13 domesticated and wild rice relatives highlight genetic conservation, turnover and innovation across the genus Oryza" (in en). Nature Genetics 50 (2): 285–296. doi:10.1038/s41588-018-0040-0. ISSN 1061-4036. http://www.nature.com/articles/s41588-018-0040-0.
- ↑ Sun, Hequan; Rowan, Beth A.; Flood, Pádraic J.; Brandt, Ronny; Fuss, Janina; Hancock, Angela M.; Michelmore, Richard W.; Huettel, Bruno et al. (1 December 2019). "Linked-read sequencing of gametes allows efficient genome-wide analysis of meiotic recombination" (in en). Nature Communications 10 (1): 4310. doi:10.1038/s41467-019-12209-2. ISSN 2041-1723. PMC PMC6754367. PMID 31541084. http://www.nature.com/articles/s41467-019-12209-2.
- ↑ Sherman, Rachel M.; Salzberg, Steven L. (1 April 2020). "Pan-genomics in the human genome era" (in en). Nature Reviews Genetics 21 (4): 243–254. doi:10.1038/s41576-020-0210-7. ISSN 1471-0056. PMC PMC7752153. PMID 32034321. http://www.nature.com/articles/s41576-020-0210-7.
- ↑ Bayer, Philipp E.; Golicz, Agnieszka A.; Scheben, Armin; Batley, Jacqueline; Edwards, David (1 August 2020). "Plant pan-genomes are the new reference" (in en). Nature Plants 6 (8): 914–920. doi:10.1038/s41477-020-0733-0. ISSN 2055-0278. http://www.nature.com/articles/s41477-020-0733-0.
- ↑ 8.0 8.1 Weckwerth, Wolfram; Ghatak, Arindam; Bellaire, Anke; Chaturvedi, Palak; Varshney, Rajeev K. (1 July 2020). "PANOMICS meets germplasm" (in en). Plant Biotechnology Journal 18 (7): 1507–1525. doi:10.1111/pbi.13372. ISSN 1467-7644. PMC PMC7292548. PMID 32163658. https://onlinelibrary.wiley.com/doi/10.1111/pbi.13372.
- ↑ Scossa, Federico; Alseekh, Saleh; Fernie, Alisdair R. (1 February 2021). "Integrating multi-omics data for crop improvement" (in en). Journal of Plant Physiology 257: 153352. doi:10.1016/j.jplph.2020.153352. https://linkinghub.elsevier.com/retrieve/pii/S017616172030242X.
- ↑ Liberman, Louisa M; Sozzani, Rosangela; Benfey, Philip N (1 April 2012). "Integrative systems biology: an attempt to describe a simple weed" (in en). Current Opinion in Plant Biology 15 (2): 162–167. doi:10.1016/j.pbi.2012.01.004. PMC PMC3435099. PMID 22277598. https://linkinghub.elsevier.com/retrieve/pii/S1369526612000052.
- ↑ 11.0 11.1 Pinu, Farhana R.; Beale, David J.; Paten, Amy M.; Kouremenos, Konstantinos; Swarup, Sanjay; Schirra, Horst J.; Wishart, David (18 April 2019). "Systems Biology and Multi-Omics Integration: Viewpoints from the Metabolomics Research Community" (in en). Metabolites 9 (4): 76. doi:10.3390/metabo9040076. ISSN 2218-1989. PMC PMC6523452. PMID 31003499. https://www.mdpi.com/2218-1989/9/4/76.
- ↑ Oberhardt, Matthew A; Palsson, Bernhard Ø; Papin, Jason A (1 January 2009). "Applications of genome‐scale metabolic reconstructions" (in en). Molecular Systems Biology 5 (1): 320. doi:10.1038/msb.2009.77. ISSN 1744-4292. PMC PMC2795471. PMID 19888215. https://onlinelibrary.wiley.com/doi/10.1038/msb.2009.77.
- ↑ Lewis, Nathan E.; Nagarajan, Harish; Palsson, Bernhard O. (1 April 2012). "Constraining the metabolic genotype–phenotype relationship using a phylogeny of in silico methods" (in en). Nature Reviews Microbiology 10 (4): 291–305. doi:10.1038/nrmicro2737. ISSN 1740-1526. PMC PMC3536058. PMID 22367118. http://www.nature.com/articles/nrmicro2737.
- ↑ Ramon, Charlotte; Gollub, Mattia G.; Stelling, Jörg (26 October 2018). "Integrating –omics data into genome-scale metabolic network models: principles and challenges" (in en). Essays in Biochemistry 62 (4): 563–574. doi:10.1042/EBC20180011. ISSN 0071-1365. https://portlandpress.com/essaysbiochem/article/62/4/563/78519/Integrating-omics-data-into-genome-scale-metabolic.
- ↑ Gomes de Oliveira Dal’Molin, Cristiana; Nielsen, Lars Keld (1 February 2018). "Plant genome-scale reconstruction: from single cell to multi-tissue modelling and omics analyses" (in en). Current Opinion in Biotechnology 49: 42–48. doi:10.1016/j.copbio.2017.07.009. https://linkinghub.elsevier.com/retrieve/pii/S0958166917301052.
- ↑ de Oliveira Dal’Molin, Cristiana Gomes; Quek, Lake-Ee; Palfreyman, Robin William; Brumbley, Stevens Michael; Nielsen, Lars Keld (1 December 2010). "C4GEM, a Genome-Scale Metabolic Model to Study C4 Plant Metabolism" (in en). Plant Physiology 154 (4): 1871–1885. doi:10.1104/pp.110.166488. ISSN 1532-2548. PMC PMC2996019. PMID 20974891. https://academic.oup.com/plphys/article/154/4/1871/6108787.
- ↑ de Oliveira Dal'Molin, Cristiana Gomes; Quek, Lake-Ee; Palfreyman, Robin William; Brumbley, Stevens Michael; Nielsen, Lars Keld (3 February 2010). "AraGEM, a Genome-Scale Reconstruction of the Primary Metabolic Network in Arabidopsis" (in en). Plant Physiology 152 (2): 579–589. doi:10.1104/pp.109.148817. ISSN 1532-2548. PMC PMC2815881. PMID 20044452. https://academic.oup.com/plphys/article/152/2/579/6108441.
- ↑ Cheung, C.Y. Maurice; Poolman, Mark G.; Fell, David. A.; Ratcliffe, R. George; Sweetlove, Lee J. (2 June 2014). "A Diel Flux Balance Model Captures Interactions between Light and Dark Metabolism during Day-Night Cycles in C3 and Crassulacean Acid Metabolism Leaves" (in en). Plant Physiology 165 (2): 917–929. doi:10.1104/pp.113.234468. ISSN 1532-2548. PMC PMC4044858. PMID 24596328. https://academic.oup.com/plphys/article/165/2/917/6113238.
- ↑ Yuan, Huili; Cheung, C.Y. Maurice; Poolman, Mark G.; Hilbers, Peter A. J.; Riel, Natal A. W. (1 January 2016). "A genome‐scale metabolic network reconstruction of tomato ( Solanum lycopersicum L.) and its application to photorespiratory metabolism" (in en). The Plant Journal 85 (2): 289–304. doi:10.1111/tpj.13075. ISSN 0960-7412. https://onlinelibrary.wiley.com/doi/10.1111/tpj.13075.
- ↑ 20.0 20.1 Simons, Margaret; Saha, Rajib; Amiour, Nardjis; Kumar, Akhil; Guillard, Lenaïg; Clément, Gilles; Miquel, Martine; Li, Zhenni et al. (5 November 2014). "Assessing the Metabolic Impact of Nitrogen Availability Using a Compartmentalized Maize Leaf Genome-Scale Model" (in en). Plant Physiology 166 (3): 1659–1674. doi:10.1104/pp.114.245787. ISSN 1532-2548. PMC PMC4226342. PMID 25248718. https://academic.oup.com/plphys/article/166/3/1659/6111218.
- ↑ Scheunemann, Michael; Brady, Siobhan M.; Nikoloski, Zoran (1 December 2018). "Integration of large-scale data for extraction of integrated Arabidopsis root cell-type specific models" (in en). Scientific Reports 8 (1): 7919. doi:10.1038/s41598-018-26232-8. ISSN 2045-2322. PMC PMC5962614. PMID 29784955. http://www.nature.com/articles/s41598-018-26232-8.
- ↑ Chang, Roger L; Ghamsari, Lila; Manichaikul, Ani; Hom, Erik F Y; Balaji, Santhanam; Fu, Weiqi; Shen, Yun; Hao, Tong et al. (1 January 2011). "Metabolic network reconstruction of Chlamydomonas offers insight into light‐driven algal metabolism" (in en). Molecular Systems Biology 7 (1): 518. doi:10.1038/msb.2011.52. ISSN 1744-4292. PMC PMC3202792. PMID 21811229. https://onlinelibrary.wiley.com/doi/10.1038/msb.2011.52.
- ↑ Chaiboonchoe, Amphun; Dohai, Bushra Saeed; Cai, Hong; Nelson, David R.; Jijakli, Kenan; Salehi-Ashtiani, Kourosh (10 December 2014). "Microalgal Metabolic Network Model Refinement through High-Throughput Functional Metabolic Profiling". Frontiers in Bioengineering and Biotechnology 2. doi:10.3389/fbioe.2014.00068. ISSN 2296-4185. PMC PMC4261833. PMID 25540776. http://journal.frontiersin.org/article/10.3389/fbioe.2014.00068/abstract.
- ↑ Shene, Carolina; Asenjo, Juan A.; Chisti, Yusuf (1 December 2018). "Metabolic modelling and simulation of the light and dark metabolism of Chlamydomonas reinhardtii" (in en). The Plant Journal 96 (5): 1076–1088. doi:10.1111/tpj.14078. https://onlinelibrary.wiley.com/doi/10.1111/tpj.14078.
- ↑ 25.0 25.1 Tong, Hao; Nikoloski, Zoran (1 February 2021). "Machine learning approaches for crop improvement: Leveraging phenotypic and genotypic big data" (in en). Journal of Plant Physiology 257: 153354. doi:10.1016/j.jplph.2020.153354. https://linkinghub.elsevier.com/retrieve/pii/S0176161720302443.
- ↑ Thiele, Ines; Palsson, Bernhard Ø (1 January 2010). "A protocol for generating a high-quality genome-scale metabolic reconstruction" (in en). Nature Protocols 5 (1): 93–121. doi:10.1038/nprot.2009.203. ISSN 1754-2189. PMC PMC3125167. PMID 20057383. http://www.nature.com/articles/nprot.2009.203.
- ↑ Salzberg, Steven L. (1 December 2019). "Next-generation genome annotation: we still struggle to get it right" (in en). Genome Biology 20 (1): 92, s13059–019–1715-2. doi:10.1186/s13059-019-1715-2. ISSN 1474-760X. PMC PMC6521345. PMID 31097009. https://genomebiology.biomedcentral.com/articles/10.1186/s13059-019-1715-2.
- ↑ Workman, Rachael E.; Tang, Alison D.; Tang, Paul S.; Jain, Miten; Tyson, John R.; Razaghi, Roham; Zuzarte, Philip C.; Gilpatrick, Timothy et al. (1 December 2019). "Nanopore native RNA sequencing of a human poly(A) transcriptome" (in en). Nature Methods 16 (12): 1297–1305. doi:10.1038/s41592-019-0617-2. ISSN 1548-7091. PMC PMC7768885. PMID 31740818. http://www.nature.com/articles/s41592-019-0617-2.
- ↑ Szecowka, Marek; Heise, Robert; Tohge, Takayuki; Nunes-Nesi, Adriano; Vosloh, Daniel; Huege, Jan; Feil, Regina; Lunn, John et al. (26 March 2013). "Metabolic Fluxes in an Illuminated Arabidopsis Rosette" (in en). The Plant Cell 25 (2): 694–714. doi:10.1105/tpc.112.106989. ISSN 1532-298X. PMC PMC3608787. PMID 23444331. https://academic.oup.com/plcell/article/25/2/694/6096534.
- ↑ Chen, Yanmei; Wang, Yi; Yang, Jun; Zhou, Wenbin; Dai, Shaojun (1 July 2021). "Exploring the diversity of plant proteome" (in en). Journal of Integrative Plant Biology 63 (7): 1197–1210. doi:10.1111/jipb.13087. ISSN 1672-9072. https://onlinelibrary.wiley.com/doi/10.1111/jipb.13087.
- ↑ Seiler, Franka; Soll, Jürgen; Bölter, Bettina (13 June 2017). "Comparative Phenotypical and Molecular Analyses of Arabidopsis Grown under Fluorescent and LED Light" (in en). Plants 6 (2): 24. doi:10.3390/plants6020024. ISSN 2223-7747. PMC PMC5489796. PMID 28608805. https://www.mdpi.com/2223-7747/6/2/24.
- ↑ Ara, Takeshi; Enomoto, Mitsuo; Arita, Masanori; Ikeda, Chiaki; Kera, Kota; Yamada, Manabu; Nishioka, Takaaki; Ikeda, Tasuku et al. (7 April 2015). "Metabolonote: A Wiki-Based Database for Managing Hierarchical Metadata of Metabolome Analyses". Frontiers in Bioengineering and Biotechnology 3. doi:10.3389/fbioe.2015.00038. ISSN 2296-4185. PMC PMC4388006. PMID 25905099. http://journal.frontiersin.org/article/10.3389/fbioe.2015.00038/abstract.
- ↑ Meyer, Rachel S. (1 July 2015). "Encouraging metadata curation in the Diversity Seek initiative" (in en). Nature Plants 1 (7): 15099. doi:10.1038/nplants.2015.99. ISSN 2055-0278. http://www.nature.com/articles/nplants201599.
- ↑ Kale, Namrata S.; Haug, Kenneth; Conesa, Pablo; Jayseelan, Kalaivani; Moreno, Pablo; Rocca‐Serra, Philippe; Nainala, Venkata Chandrasekhar; Spicer, Rachel A. et al. (1 March 2016). "MetaboLights: An Open‐Access Database Repository for Metabolomics Data" (in en). Current Protocols in Bioinformatics 53 (1). doi:10.1002/0471250953.bi1413s53. ISSN 1934-3396. https://onlinelibrary.wiley.com/doi/10.1002/0471250953.bi1413s53.
- ↑ Sulpice, Ronan; Flis, Anna; Ivakov, Alexander A.; Apelt, Federico; Krohn, Nicole; Encke, Beatrice; Abel, Christin; Feil, Regina et al. (1 January 2014). "Arabidopsis Coordinates the Diurnal Regulation of Carbon Allocation and Growth across a Wide Range of Photoperiods" (in en). Molecular Plant 7 (1): 137–155. doi:10.1093/mp/sst127. https://linkinghub.elsevier.com/retrieve/pii/S1674205214608601.
- ↑ Weiszmann, Jakob; Fürtauer, Lisa; Weckwerth, Wolfram; Nägele, Thomas (1 November 2018). "Vacuolar sucrose cleavage prevents limitation of cytosolic carbohydrate metabolism and stabilizes photosynthesis under abiotic stress" (in en). The FEBS Journal 285 (21): 4082–4098. doi:10.1111/febs.14656. ISSN 1742-464X. https://onlinelibrary.wiley.com/doi/10.1111/febs.14656.
- ↑ Fernie, Alisdair R.; Trethewey, Richard N.; Krotzky, Arno J.; Willmitzer, Lothar (1 September 2004). "Metabolite profiling: from diagnostics to systems biology" (in en). Nature Reviews Molecular Cell Biology 5 (9): 763–769. doi:10.1038/nrm1451. ISSN 1471-0072. http://www.nature.com/articles/nrm1451.
- ↑ Fang, Chuanying; Fernie, Alisdair R.; Luo, Jie (1 January 2019). "Exploring the Diversity of Plant Metabolism" (in en). Trends in Plant Science 24 (1): 83–98. doi:10.1016/j.tplants.2018.09.006. https://linkinghub.elsevier.com/retrieve/pii/S1360138518302115.
- ↑ Pazhamala, Lekha T.; Kudapa, Himabindu; Weckwerth, Wolfram; Millar, A. Harvey; Varshney, Rajeev K. (1 July 2021). "Systems biology for crop improvement" (in en). The Plant Genome 14 (2). doi:10.1002/tpg2.20098. ISSN 1940-3372. https://onlinelibrary.wiley.com/doi/10.1002/tpg2.20098.
- ↑ Zancarini, Anouk; Westerhuis, Johan A; Smilde, Age K; Bouwmeester, Harro J (1 August 2021). "Integration of omics data to unravel root microbiome recruitment" (in en). Current Opinion in Biotechnology 70: 255–261. doi:10.1016/j.copbio.2021.06.016. https://linkinghub.elsevier.com/retrieve/pii/S0958166921001002.
- ↑ De Vijlder, Thomas; Valkenborg, Dirk; Lemière, Filip; Romijn, Edwin P.; Laukens, Kris; Cuyckens, Filip (1 September 2018). "A tutorial in small molecule identification via electrospray ionization-mass spectrometry: The practical art of structural elucidation" (in en). Mass Spectrometry Reviews 37 (5): 607–629. doi:10.1002/mas.21551. PMC PMC6099382. PMID 29120505. https://onlinelibrary.wiley.com/doi/10.1002/mas.21551.
- ↑ Webb, Sarah (1 February 2018). "Deep learning for biology" (in en). Nature 554 (7693): 555–557. doi:10.1038/d41586-018-02174-z. ISSN 0028-0836. http://www.nature.com/articles/d41586-018-02174-z.
- ↑ Karp, Peter D. (2016). "Can we replace curation with information extraction software?" (in en). Database 2016: baw150. doi:10.1093/database/baw150. ISSN 1758-0463. PMC PMC5199131. PMID 28025341. https://academic.oup.com/database/article-lookup/doi/10.1093/database/baw150.
- ↑ The UniProt Consortium (8 January 2019). "UniProt: a worldwide hub of protein knowledge" (in en). Nucleic Acids Research 47 (D1): D506–D515. doi:10.1093/nar/gky1049. ISSN 0305-1048. PMC PMC6323992. PMID 30395287. https://academic.oup.com/nar/article/47/D1/D506/5160987.
- ↑ Bolser, Dan; Staines, Daniel M.; Pritchard, Emily; Kersey, Paul (2016), Edwards, David, ed., "Ensembl Plants: Integrating Tools for Visualizing, Mining, and Analyzing Plant Genomics Data", Plant Bioinformatics (New York, NY: Springer New York) 1374: 115–140, doi:10.1007/978-1-4939-3167-5_6, ISBN 978-1-4939-3166-8, http://link.springer.com/10.1007/978-1-4939-3167-5_6. Retrieved 2021-12-17
- ↑ Van Bel, Michiel; Diels, Tim; Vancaester, Emmelien; Kreft, Lukasz; Botzki, Alexander; Van de Peer, Yves; Coppens, Frederik; Vandepoele, Klaas (4 January 2018). "PLAZA 4.0: an integrative resource for functional, evolutionary and comparative plant genomics" (in en). Nucleic Acids Research 46 (D1): D1190–D1196. doi:10.1093/nar/gkx1002. ISSN 0305-1048. PMC PMC5753339. PMID 29069403. http://academic.oup.com/nar/article/46/D1/D1190/4561641.
- ↑ Berardini, Tanya Z.; Reiser, Leonore; Li, Donghui; Mezheritsky, Yarik; Muller, Robert; Strait, Emily; Huala, Eva (1 August 2015). "The arabidopsis information resource: Making and mining the “gold standard” annotated reference plant genome: Tair: Making and Mining the “Gold Standard” Plant Genome" (in en). genesis 53 (8): 474–485. doi:10.1002/dvg.22877. PMC PMC4545719. PMID 26201819. https://onlinelibrary.wiley.com/doi/10.1002/dvg.22877.
- ↑ Krishnakumar, Vivek; Hanlon, Matthew R.; Contrino, Sergio; Ferlanti, Erik S.; Karamycheva, Svetlana; Kim, Maria; Rosen, Benjamin D.; Cheng, Chia-Yi et al. (28 January 2015). "Araport: the Arabidopsis Information Portal" (in en). Nucleic Acids Research 43 (D1): D1003–D1009. doi:10.1093/nar/gku1200. ISSN 1362-4962. PMC PMC4383980. PMID 25414324. http://academic.oup.com/nar/article/43/D1/D1003/2439074/Araport-the-Arabidopsis-Information-Portal.
- ↑ Schwacke, Rainer; Schneider, Anja; van der Graaff, Eric; Fischer, Karsten; Catoni, Elisabetta; Desimone, Marcelo; Frommer, Wolf B.; Flügge, Ulf-Ingo et al. (1 January 2003). "ARAMEMNON, a Novel Database for Arabidopsis Integral Membrane Proteins" (in en). Plant Physiology 131 (1): 16–26. doi:10.1104/pp.011577. ISSN 1532-2548. PMC PMC166783. PMID 12529511. https://academic.oup.com/plphys/article/131/1/16/6114365.
- ↑ Goodstein, David M.; Shu, Shengqiang; Howson, Russell; Neupane, Rochak; Hayes, Richard D.; Fazo, Joni; Mitros, Therese; Dirks, William et al. (1 January 2012). "Phytozome: a comparative platform for green plant genomics" (in en). Nucleic Acids Research 40 (D1): D1178–D1186. doi:10.1093/nar/gkr944. ISSN 1362-4962. PMC PMC3245001. PMID 22110026. https://academic.oup.com/nar/article-lookup/doi/10.1093/nar/gkr944.
- ↑ Vizcaíno, Juan A; Deutsch, Eric W; Wang, Rui; Csordas, Attila; Reisinger, Florian; Ríos, Daniel; Dianes, José A; Sun, Zhi et al. (1 March 2014). "ProteomeXchange provides globally coordinated proteomics data submission and dissemination" (in en). Nature Biotechnology 32 (3): 223–226. doi:10.1038/nbt.2839. ISSN 1087-0156. PMC PMC3986813. PMID 24727771. http://www.nature.com/articles/nbt.2839.
- ↑ Clough, Emily; Barrett, Tanya (2016), Mathé, Ewy; Davis, Sean, eds., "The Gene Expression Omnibus Database", Statistical Genomics (New York, NY: Springer New York) 1418: 93–110, doi:10.1007/978-1-4939-3578-9_5, ISBN 978-1-4939-3576-5, PMC PMC4944384, PMID 27008011, http://link.springer.com/10.1007/978-1-4939-3578-9_5. Retrieved 2021-12-17
- ↑ Leinonen, R.; Sugawara, H.; Shumway, M.; on behalf of the International Nucleotide Sequence Database Collaboration (1 January 2011). "The Sequence Read Archive" (in en). Nucleic Acids Research 39 (Database): D19–D21. doi:10.1093/nar/gkq1019. ISSN 0305-1048. PMC PMC3013647. PMID 21062823. https://academic.oup.com/nar/article-lookup/doi/10.1093/nar/gkq1019.
- ↑ Haug, Kenneth; Salek, Reza M.; Conesa, Pablo; Hastings, Janna; de Matos, Paula; Rijnbeek, Mark; Mahendraker, Tejasvi; Williams, Mark et al. (1 January 2013). "MetaboLights—an open-access general-purpose repository for metabolomics studies and associated meta-data" (in en). Nucleic Acids Research 41 (D1): D781–D786. doi:10.1093/nar/gks1004. ISSN 0305-1048. PMC PMC3531110. PMID 23109552. http://academic.oup.com/nar/article/41/D1/D781/1050654/MetaboLightsan-openaccess-generalpurpose.
- ↑ Taylor, Chris F; Field, Dawn; Sansone, Susanna-Assunta; Aerts, Jan; Apweiler, Rolf; Ashburner, Michael; Ball, Catherine A; Binz, Pierre-Alain et al. (1 August 2008). "Promoting coherent minimum reporting guidelines for biological and biomedical investigations: the MIBBI project" (in en). Nature Biotechnology 26 (8): 889–896. doi:10.1038/nbt.1411. ISSN 1087-0156. PMC PMC2771753. PMID 18688244. http://www.nature.com/articles/nbt.1411.
- ↑ Zimmermann, Philip; Schildknecht, Beatrice; Craigon, David; Garcia-Hernandez, Margarita; Gruissem, Wilhelm; May, Sean; Mukherjee, Gaurab; Parkinson, Helen et al. (1 December 2006). "MIAME/Plant – adding value to plant microarrray experiments" (in en). Plant Methods 2 (1): 1. doi:10.1186/1746-4811-2-1. ISSN 1746-4811. PMC PMC1334190. PMID 16401339. https://plantmethods.biomedcentral.com/articles/10.1186/1746-4811-2-1.
- ↑ Krajewski, Paweł; Chen, Dijun; Ćwiek, Hanna; van Dijk, Aalt D.J.; Fiorani, Fabio; Kersey, Paul; Klukas, Christian; Lange, Matthias et al. (1 September 2015). "Towards recommendations for metadata and data handling in plant phenotyping" (in en). Journal of Experimental Botany 66 (18): 5417–5427. doi:10.1093/jxb/erv271. ISSN 0022-0957. https://academic.oup.com/jxb/article-lookup/doi/10.1093/jxb/erv271.
- ↑ Leonelli, Sabina (5 April 2019). "The challenges of big data biology" (in en). eLife 8: e47381. doi:10.7554/eLife.47381. ISSN 2050-084X. PMC PMC6450665. PMID 30950793. https://elifesciences.org/articles/47381.
- ↑ Wilkinson, Mark D.; Dumontier, Michel; Aalbersberg, IJsbrand Jan; Appleton, Gabrielle; Axton, Myles; Baak, Arie; Blomberg, Niklas; Boiten, Jan-Willem et al. (1 December 2016). "The FAIR Guiding Principles for scientific data management and stewardship" (in en). Scientific Data 3 (1): 160018. doi:10.1038/sdata.2016.18. ISSN 2052-4463. PMC PMC4792175. PMID 26978244. http://www.nature.com/articles/sdata201618.
- ↑ Hettne, Kristina M; Dharuri, Harish; Zhao, Jun; Wolstencroft, Katherine; Belhajjame, Khalid; Soiland-Reyes, Stian; Mina, Eleni; Thompson, Mark et al. (1 December 2014). "Structuring research methods and data with the research object model: genomics workflows as a case study" (in en). Journal of Biomedical Semantics 5 (1): 41. doi:10.1186/2041-1480-5-41. ISSN 2041-1480. PMC PMC4177597. PMID 25276335. https://jbiomedsem.biomedcentral.com/articles/10.1186/2041-1480-5-41.
- ↑ Carragáin, Eoghan Ó; Goble, Carole; Sefton, Peter; Soiland-Reyes, Stian (20 June 2019). A lightweight approach to research object data packaging. doi:10.5281/ZENODO.3250687. https://zenodo.org/record/3250687.
- ↑ González-Beltrán, Alejandra; Maguire, Eamonn; Sansone, Susanna-Assunta; Rocca-Serra, Philippe (1 December 2014). "linkedISA: semantic representation of ISA-Tab experimental metadata" (in en). BMC Bioinformatics 15 (S14): S4. doi:10.1186/1471-2105-15-S14-S4. ISSN 1471-2105. PMC PMC4255742. PMID 25472428. https://bmcbioinformatics.biomedcentral.com/articles/10.1186/1471-2105-15-S14-S4.
- ↑ 63.0 63.1 Simonyan, Vahan; Goecks, Jeremy; Mazumder, Raja (2017). "Biocompute Objects—A Step towards Evaluation and Validation of Biomedical Scientific Computations" (in en). PDA Journal of Pharmaceutical Science and Technology 71 (2): 136–146. doi:10.5731/pdajpst.2016.006734. ISSN 1079-7440. PMC PMC5510742. PMID 27974626. http://journal.pda.org/lookup/doi/10.5731/pdajpst.2016.006734.
- ↑ Vicente-Saez, Ruben; Martinez-Fuentes, Clara (1 July 2018). "Open Science now: A systematic literature review for an integrated definition" (in en). Journal of Business Research 88: 428–436. doi:10.1016/j.jbusres.2017.12.043. https://linkinghub.elsevier.com/retrieve/pii/S0148296317305441.
- ↑ 65.0 65.1 65.2 Skansi, S. (2018). Introduction to deep learning. New York, NY: Springer Berlin Heidelberg. ISBN 978-3-319-73003-5.
- ↑ Li, Yifeng; Wu, Fang-Xiang; Ngom, Alioune (22 December 2016). "A review on machine learning principles for multi-view biological data integration" (in en). Briefings in Bioinformatics: bbw113. doi:10.1093/bib/bbw113. ISSN 1467-5463. https://academic.oup.com/bib/article-lookup/doi/10.1093/bib/bbw113.
- ↑ Sun, Shanwen; Wang, Chunyu; Ding, Hui; Zou, Quan (22 January 2020). "Machine learning and its applications in plant molecular studies" (in en). Briefings in Functional Genomics 19 (1): 40–48. doi:10.1093/bfgp/elz036. ISSN 2041-2657. https://academic.oup.com/bfg/article/19/1/40/5682485.
- ↑ Dong, Hao; Ding, Zihan; Zhang, Shanghang (2020) (in English). Deep Reinforcement Learning Fundamentals, Research and Applications. ISBN 978-981-15-4095-0. OCLC 1287882129. https://www.worldcat.org/title/mediawiki/oclc/1287882129.
- ↑ Shteingart, Hanan; Loewenstein, Yonatan (1 April 2014). "Reinforcement learning and human behavior" (in en). Current Opinion in Neurobiology 25: 93–98. doi:10.1016/j.conb.2013.12.004. https://linkinghub.elsevier.com/retrieve/pii/S0959438813002286.
- ↑ Esteva, Andre; Robicquet, Alexandre; Ramsundar, Bharath; Kuleshov, Volodymyr; DePristo, Mark; Chou, Katherine; Cui, Claire; Corrado, Greg et al. (1 January 2019). "A guide to deep learning in healthcare" (in en). Nature Medicine 25 (1): 24–29. doi:10.1038/s41591-018-0316-z. ISSN 1078-8956. http://www.nature.com/articles/s41591-018-0316-z.
- ↑ Koch, Mathilde; Duigou, Thomas; Faulon, Jean-Loup (17 January 2020). "Reinforcement Learning for Bioretrosynthesis" (in en). ACS Synthetic Biology 9 (1): 157–168. doi:10.1021/acssynbio.9b00447. ISSN 2161-5063. https://pubs.acs.org/doi/10.1021/acssynbio.9b00447.
- ↑ 72.0 72.1 Bhattacharyya, Siddhartha, ed. (2020). Deep learning: research and applications. De Gruyter frontiers in computational intelligence. Boston: De Gruyter. ISBN 978-3-11-067079-0.
- ↑ Senior, Andrew W.; Evans, Richard; Jumper, John; Kirkpatrick, James; Sifre, Laurent; Green, Tim; Qin, Chongli; Žídek, Augustin et al. (30 January 2020). "Improved protein structure prediction using potentials from deep learning" (in en). Nature 577 (7792): 706–710. doi:10.1038/s41586-019-1923-7. ISSN 0028-0836. http://www.nature.com/articles/s41586-019-1923-7.
- ↑ Zimmer, David; Schneider, Kevin; Sommer, Frederik; Schroda, Michael; Mühlhaus, Timo (13 November 2018). "Artificial Intelligence Understands Peptide Observability and Assists With Absolute Protein Quantification". Frontiers in Plant Science 9: 1559. doi:10.3389/fpls.2018.01559. ISSN 1664-462X. PMC PMC6242780. PMID 30483279. https://www.frontiersin.org/article/10.3389/fpls.2018.01559/full.
- ↑ 75.0 75.1 75.2 Wang, Hai; Cimen, Emre; Singh, Nisha; Buckler, Edward (1 April 2020). "Deep learning for plant genomics and crop improvement" (in en). Current Opinion in Plant Biology 54: 34–41. doi:10.1016/j.pbi.2019.12.010. https://linkinghub.elsevier.com/retrieve/pii/S1369526619301256.
- ↑ Khaki, Saeed; Wang, Lizhi (22 May 2019). "Crop Yield Prediction Using Deep Neural Networks". Frontiers in Plant Science 10: 621. doi:10.3389/fpls.2019.00621. ISSN 1664-462X. PMC PMC6540942. PMID 31191564. https://www.frontiersin.org/article/10.3389/fpls.2019.00621/full.
- ↑ Tong, Hao; Küken, Anika; Nikoloski, Zoran (1 December 2020). "Integrating molecular markers into metabolic models improves genomic selection for Arabidopsis growth" (in en). Nature Communications 11 (1): 2410. doi:10.1038/s41467-020-16279-5. ISSN 2041-1723. PMC PMC7229213. PMID 32415110. http://www.nature.com/articles/s41467-020-16279-5.
- ↑ Xu, Chunming; Jackson, Scott A. (1 December 2019). "Machine learning and complex biological data" (in en). Genome Biology 20 (1): 76, s13059–019–1689-0. doi:10.1186/s13059-019-1689-0. ISSN 1474-760X. PMC PMC6469083. PMID 30992073. https://genomebiology.biomedcentral.com/articles/10.1186/s13059-019-1689-0.
- ↑ Fürtauer, Lisa; Küstner, Lisa; Weckwerth, Wolfram; Heyer, Arnd G.; Nägele, Thomas (1 November 2019). "Resolving subcellular plant metabolism" (in en). The Plant Journal 100 (3): 438–455. doi:10.1111/tpj.14472. ISSN 0960-7412. https://onlinelibrary.wiley.com/doi/10.1111/tpj.14472.
- ↑ Andrews, Steven S.; Arkin, Adam P. (1 July 2006). "Simulating cell biology" (in en). Current Biology 16 (14): R523–R527. doi:10.1016/j.cub.2006.06.048. https://linkinghub.elsevier.com/retrieve/pii/S0960982206017751.
- ↑ Rohwer, Johann M. (1 March 2012). "Kinetic modelling of plant metabolic pathways" (in en). Journal of Experimental Botany 63 (6): 2275–2292. doi:10.1093/jxb/ers080. ISSN 1460-2431. https://academic.oup.com/jxb/article-lookup/doi/10.1093/jxb/ers080.
- ↑ Nägele, Thomas (6 November 2014). "Linking metabolomics data to underlying metabolic regulation". Frontiers in Molecular Biosciences 1. doi:10.3389/fmolb.2014.00022. ISSN 2296-889X. PMC PMC4428386. PMID 25988163. http://journal.frontiersin.org/article/10.3389/fmolb.2014.00022/abstract.
- ↑ Hoops, S.; Sahle, S.; Gauges, R.; Lee, C.; Pahle, J.; Simus, N.; Singhal, M.; Xu, L. et al. (15 December 2006). "COPASI--a COmplex PAthway SImulator" (in en). Bioinformatics 22 (24): 3067–3074. doi:10.1093/bioinformatics/btl485. ISSN 1367-4803. https://academic.oup.com/bioinformatics/article-lookup/doi/10.1093/bioinformatics/btl485.
- ↑ Kent, Edward; Hoops, Stefan; Mendes, Pedro (1 December 2012). "Condor-COPASI: high-throughput computing for biochemical networks" (in en). BMC Systems Biology 6 (1): 91. doi:10.1186/1752-0509-6-91. ISSN 1752-0509. PMC PMC3527284. PMID 22834945. https://bmcsystbiol.biomedcentral.com/articles/10.1186/1752-0509-6-91.
- ↑ van Rossum, G.; Drake Jr., F.L. (1995). Python Tutorial. 620. Centrum voor Wiskunde en Informatica.
- ↑ R Core Team (2021). "R: A Language and Environment for Statistical Computing". R Foundation for Statistical Computing. https://www.r-project.org/. Retrieved 16 August 2021.
- ↑ Moles, Carmen G.; Mendes, Pedro; Banga, Julio R. (1 November 2003). "Parameter Estimation in Biochemical Pathways: A Comparison of Global Optimization Methods" (in en). Genome Research 13 (11): 2467–2474. doi:10.1101/gr.1262503. ISSN 1088-9051. PMC PMC403766. PMID 14559783. http://genome.cshlp.org/lookup/doi/10.1101/gr.1262503.
- ↑ Gutenkunst, Ryan N; Waterfall, Joshua J; Casey, Fergal P; Brown, Kevin S; Myers, Christopher R; Sethna, James P (5 October 2007). Arkin, Adam P. ed. "Universally Sloppy Parameter Sensitivities in Systems Biology Models" (in en). PLoS Computational Biology 3 (10): e189. doi:10.1371/journal.pcbi.0030189. ISSN 1553-7358. PMC PMC2000971. PMID 17922568. https://dx.plos.org/10.1371/journal.pcbi.0030189.
- ↑ Liebermeister, W.; Schaber, J.; Klipp, E. (1 January 2009). "Nested uncertainties in biochemical models" (in en). IET Systems Biology 3 (1): 1–9. doi:10.1049/iet-syb:20070042. ISSN 1751-8849. https://digital-library.theiet.org/content/journals/10.1049/iet-syb_20070042.
- ↑ Babtie, Ann C.; Stumpf, Michael P. H. (1 August 2017). "How to deal with parameters for whole-cell modelling" (in en). Journal of The Royal Society Interface 14 (133): 20170237. doi:10.1098/rsif.2017.0237. ISSN 1742-5689. PMC PMC5582120. PMID 28768879. https://royalsocietypublishing.org/doi/10.1098/rsif.2017.0237.
- ↑ Krantz, Maria; Klipp, Edda (1 January 2020). "Moonlighting proteins - an approach to systematize the concept" (in en). In Silico Biology 13 (3-4): 71–83. doi:10.3233/ISB-190473. ISSN 1386-6338. PMC PMC7505007. PMID 32285845. https://content.iospress.com/articles/in-silico-biology/isb190473.
- ↑ Ruoff, Peter; Zakhartsev, Maxim; Westerhoff, Hans V. (1 February 2007). "Temperature compensation through systems biology: Temperature compensation of fluxes" (in en). The FEBS Journal 274 (4): 940–950. doi:10.1111/j.1742-4658.2007.05641.x. https://onlinelibrary.wiley.com/doi/10.1111/j.1742-4658.2007.05641.x.
- ↑ Pokhilko, Alexandra; Flis, Anna; Sulpice, Ronan; Stitt, Mark; Ebenhöh, Oliver (2014). "Adjustment of carbon fluxes to light conditions regulates the daily turnover of starch in plants: a computational model" (in en). Mol. BioSyst. 10 (3): 613–627. doi:10.1039/C3MB70459A. ISSN 1742-206X. http://xlink.rsc.org/?DOI=C3MB70459A.
Notes
This presentation is faithful to the original, with only a few minor changes to presentation, spelling, and grammar. In some cases important information was missing from the references, and that information was added. The original article lists references in alphabetical order; however, this version lists them in order of appearance, by design.
- LIMSwiki journal articles (added in 2021)
- LIMSwiki journal articles (all)
- LIMSwiki journal articles (with rendered math)
- LIMSwiki journal articles on clinical informatics
- LIMSwiki journal articles on FAIR data principles
- LIMSwiki journal articles on laboratory management
- LIMSwiki journal articles on pathology informatics